题目内容
17.定义运算$|{\begin{array}{l}a&b\\ c&d\end{array}}|=ad-bc$,若$|{\begin{array}{l}{sinθ}&2\\{cosθ}&3\end{array}}|=0$,则2sin2θ+sinθcosθ的值是$\frac{14}{13}$.分析 根据题意得出3sinθ-2cosθ=0,再化2sin2θ+sinθcosθ=$\frac{{2sin}^{2}θ+sinθcosθ}{{sin}^{2}θ{+cos}^{2}θ}$,代入求值即可.
解答 解:根据题意,$|{\begin{array}{l}{sinθ}&2\\{cosθ}&3\end{array}}|=0$,
∴3sinθ-2cosθ=0,
∴tanθ=$\frac{sinθ}{cosθ}$=$\frac{2}{3}$,
∴2sin2θ+sinθcosθ=$\frac{{2sin}^{2}θ+sinθcosθ}{{sin}^{2}θ{+cos}^{2}θ}$
=$\frac{{2tan}^{2}θ+tanθ}{{tan}^{2}θ+1}$
=$\frac{2{×(\frac{2}{3})}^{2}+\frac{2}{3}}{{(\frac{2}{3})}^{2}+1}$
=$\frac{14}{13}$.
故答案为:$\frac{14}{13}$.
点评 本题考查了新定义的三角函数化简与求值问题,是基础题.

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
19.“x≥1”是“lgx≥0”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
5.函数f(x)=$\frac{A}{sin(ωx+φ)}(A>0,ω>0,|φ|<\frac{π}{2})$的部分图象如图所示,则$f(\frac{3π}{2})$=( )
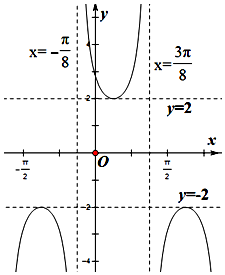

| A. | $2\sqrt{3}$ | B. | $-2\sqrt{3}$ | C. | $2\sqrt{2}$ | D. | $-2\sqrt{2}$ |
12.已知三条直线a、b、c两两平行且不共面,这三条直线可以确定m个平面,这m个平面把空间分成n个部分,则( )
| A. | m=2 n=2 | B. | m=2 n=6 | C. | m=3 n=7 | D. | m=3 n=8 |
2.已知全集U={1,2,3,4},集合A={1,3,4},B={2,3},则A∩(∁UB)=( )
| A. | {2} | B. | {1,4} | C. | {3} | D. | {1,2,3,4} |
6.一个几何体的三视图如图所示,则这个几何体的表面积为( )
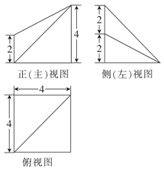

| A. | 40+8$\sqrt{2}$+4$\sqrt{6}$ | B. | 40+8$\sqrt{3}$+4$\sqrt{6}$ | C. | 48+8$\sqrt{3}$ | D. | 48+8$\sqrt{2}$ |