题目内容
1.已知数列{an}满足a1=-1,${a_{2n}}-{a_{2n-1}}={2^{2n-1}}$,${a_{2n+1}}-{a_{2n}}={2^{2n}}$,则a10=1021.分析 数列{an}满足a1=-1,${a_{2n}}-{a_{2n-1}}={2^{2n-1}}$,${a_{2n+1}}-{a_{2n}}={2^{2n}}$,可得a10=(a10-a9)+(a9-a8)+…+(a2-a1)+a1,即可得出.
解答 解:∵数列{an}满足a1=-1,${a_{2n}}-{a_{2n-1}}={2^{2n-1}}$,${a_{2n+1}}-{a_{2n}}={2^{2n}}$,
则a10=(a10-a9)+(a9-a8)+…+(a2-a1)+a1
=29+28+…+2-1
=$\frac{2({2}^{9}-1)}{2-1}$-1
=1021
故答案为:1021.
点评 本题考查了数列递推关系、等比数列的求和公式、“累加求和”方法,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
12.已知三条直线a、b、c两两平行且不共面,这三条直线可以确定m个平面,这m个平面把空间分成n个部分,则( )
| A. | m=2 n=2 | B. | m=2 n=6 | C. | m=3 n=7 | D. | m=3 n=8 |
6.一个几何体的三视图如图所示,则这个几何体的表面积为( )
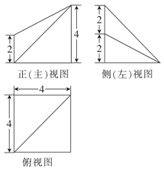

| A. | 40+8$\sqrt{2}$+4$\sqrt{6}$ | B. | 40+8$\sqrt{3}$+4$\sqrt{6}$ | C. | 48+8$\sqrt{3}$ | D. | 48+8$\sqrt{2}$ |
11.已知正数a,b,c满足5c-3a≤b≤4c-a,b≥c,则$\frac{b}{a}$的取值范围为( )
| A. | [2,7] | B. | (0,7] | C. | [$\frac{1}{3}$,7] | D. | [3,7] |