题目内容
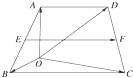如图，在梯形ABCD中，AD∥BC，| OA |
| a |
| OB |
| b |
| OC |
| c |
| OD |
| d |
A、
| ||||||||||||
B、
| ||||||||||||
C、
| ||||||||||||
D、
|
考点：向量加减混合运算及其几何意义
专题：平面向量及应用
分析：由于EF为梯形ABCD的中位线，AD∥BC，可得
=
(
+
)，利用三角形法则可得
=
-
=
-
，
=
-
=
-
，代入即可得出．
| EF |
| 1 |
| 2 |
| AD |
| BC |
| AD |
| OD |
| OA |
| d |
| a |
| BC |
| OC |
| OB |
| c |
| b |
解答：
解：∵EF为梯形ABCD的中位线，AD∥BC，
∴
=
(
+
)，
又
=
-
=
-
，
=
-
=
-
，
∴
=
(
+
-
-
)．
故选：C．
∴
| EF |
| 1 |
| 2 |
| AD |
| BC |
又
| AD |
| OD |
| OA |
| d |
| a |
| BC |
| OC |
| OB |
| c |
| b |
∴
| EF |
| 1 |
| 2 |
| c |
| d |
| a |
| b |
故选：C．
点评：本题考查了梯形的中位线定理、向量的三角形法则，属于基础题．
练习册系列答案
名师指导期末冲刺卷系列答案
相关题目
设集合A={-1，2}，B={x|
＜（
）x＜4}，则A∩B=（ ）
| 1 |
| 2 |
| 1 |
| 2 |
| A、{-1，0} | B、{-1} |
| C、{0} | D、{0，1} |
已知|
|=6，|
|=3，
•
=-12，则向量
在向量
方向上的投影是（ ）
| a |
| b |
| a |
| b |
| a |
| b |
| A、2 | B、-2 | C、4 | D、-4 |
命题“?x∈[1，3]，x2-a≤0”为真命题的一个充分不必要条件是（ ）
| A、a≥9 | B、a≤9 |
| C、a≥10 | D、a≤10 |
下列函数在（1，+∞）为增函数的是（ ）
| A、y=x2-4x | ||
| B、y=|x-2| | ||
C、y=
| ||
| D、y=log0.5x |
cos75°cos15°+sin75°sin15°的值为（ ）
| A、0 | ||||
B、
| ||||
C、
| ||||
| D、1 |
不等式x2-x-6＞0的解集是（ ）
| A、{x|-2＜x＜3} |
| B、{x|x＜-2或x＞3} |
| C、{x|-3＜x＜2} |
| D、{x|x＜-3或x＞2} |