题目内容
已知|
|=6，|
|=3，
•
=-12，则向量
在向量
方向上的投影是（ ）
| a |
| b |
| a |
| b |
| a |
| b |
| A、2 | B、-2 | C、4 | D、-4 |
考点：平面向量数量积的运算
专题：平面向量及应用
分析：向量
在向量
方向上的投影为|
|cos＜
，
＞=
，代入数值计算即可．
| a |
| b |
| a |
| a |
| b |
| ||||
|
|
解答：
解：向量
在向量
方向上的投影为：
|
|cos＜
，
＞=
=
=-4
故选：D
| a |
| b |
|
| a |
| a |
| b |
| ||||
|
|
| -12 |
| 3 |
故选：D
点评：本题考查向量投影的求法，属基础题．
练习册系列答案
相关题目
已知向量
=（2，1），
=（-3，4），则
-
的坐标为（ ）
| a |
| b |
| a |
| b |
| A、（-5，3） |
| B、（-1，5） |
| C、（5，-3） |
| D、（1，-5） |
设A={0，1}，B={x|x∈A}，则集合A与B的关系是（ ）
| A、A?B | B、B?A |
| C、A=B | D、A∈B |
若直线ax-2y-1=0与直线x+y-2=0互相垂直，则a的值为（ ）
A、-
| ||
B、
| ||
| C、-2 | ||
| D、2 |
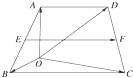如图，在梯形ABCD中，AD∥BC，| OA |
| a |
| OB |
| b |
| OC |
| c |
| OD |
| d |
A、
| ||||||||||||
B、
| ||||||||||||
C、
| ||||||||||||
D、
|
数列{an}是首项为m、公比为q（q≠1）的等比数列，Sn是它的前n项和，对任意的n∈N，点（an，
）（ ）
| S2n |
| Sn |
| A、在直线mx+qy-q=0上 |
| B、在直线qx-my+m=0上 |
| C、在直线qx+my-q=0上 |
| D、不一定在一条直线上 |