题目内容

设集合A={-1，2}，B={x|
1
2
＜（
1
2
）x＜4}，则A∩B=（　　）
A、{-1，0}B、{-1}
C、{0}D、{0，1}
考点：交集及其运算
专题：计算题,不等式的解法及应用
分析：通过解不等式求得集合B，利用交集的定义求A∩B．
解答： 解：由
1
2
＜（
1
2
）x＜4得：-2＜x＜1，
∴A∩B={-1}，
故答案为：B．
点评：本题考查了交集及其运算，熟练掌握交集的定义是解题的关键．
练习册系列答案
相关题目
在四边形ABCD中，
AB
=
a
，
BC
=
b
，
CD
=
c
，
DA
=
d
，若
a
•
b
=
b
•
c
=
c
•
d
=
d
•
a
且|
a
+
b
|=2，|
b
|=
1
3
|
a
|，则四边形ABCD的面积为
 
．
若将圆x2+y2=π2内的正弦曲线y=sinx与x轴围成的区域记为M，则在圆内随机放一粒豆子，落入M的概率
 
．
复数
1-2i
3+4i
的共轭复数在复平面上对应的点应在第
 
象限．
已知二次函数f（x）=-x2+ax-4，若对任意的x∈R，f（x）≤0，则a的取值范围是（用区间表示）．
已知向量
a
=（2，1），
b
=（-3，4），则
a
-
b
的坐标为（　　）
A、（-5，3）
B、（-1，5）
C、（5，-3）
D、（1，-5）
设A={0，1}，B={x|x∈A}，则集合A与B的关系是（　　）
A、A?BB、B?A
C、A=BD、A∈B
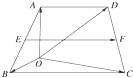如图，在梯形ABCD中，AD∥BC，
OA
=
a
，
OB
=
b
，
OC
=
c
，
OD
=
d
，且E、F分别为AB、CD的中点，则（　　）
A、
EF
=
1
2
（
a
+
b
+
c
+
d
）
B、
EF
=
1
2
（
a
-
b
+
c
-
d
）
C、
EF
=
1
2
（
c
+
d
-
a
-
b
）
D、
EF
=
1
2
（
a
+
b
-
c
-
d
）
若x＞0，则 x+
1
x
的最小值为（　　）
A、4B、3C、2D、1

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网