题目内容
15.已知函数f(x)=(2-a)(x-1)-2lnx,a∈R.(Ⅰ)若a=1,求曲线y=f(x)在点(1,f(1))处的切线方程;
(Ⅱ)若不等式f(x)>0在区间(0,$\frac{1}{2}$)上恒成立,求实数a的取值范围.
分析 (Ⅰ)求出函数的导数,计算f(1),f′(1)的值,求出切线方程即可;
(Ⅱ)问题转化为a>2-$\frac{2lnx}{x-1}$在(0,$\frac{1}{2}$)恒成立,令h(x)=2-$\frac{2lnx}{x-1}$,x∈(0,$\frac{1}{2}$),根据函数的单调性求出a的范围即可.
解答 解:(Ⅰ)a=1时,f(x)=x-1-2lnx,f′(x)=1-$\frac{2}{x}$,
故f(1)=0,f′(1)=-1,
故切线方程是:y=-(x-1),
即x+y-1=0.
(Ⅱ)若不等式f(x)>0在区间(0,$\frac{1}{2}$)上恒成立,
即a>2-$\frac{2lnx}{x-1}$在(0,$\frac{1}{2}$)恒成立,
令h(x)=2-$\frac{2lnx}{x-1}$,x∈(0,$\frac{1}{2}$),
则h′(x)=-2•$\frac{1-\frac{1}{x}-lnx}{{(x-1)}^{2}}$,
令m(x)=1-$\frac{1}{x}$-lnx,x∈(0,$\frac{1}{2}$),
则m′(x)=$\frac{1-x}{{x}^{2}}$>0,m(x)在(0,$\frac{1}{2}$)递增,
故m(x)<m($\frac{1}{2}$)=-1+ln2<0,
故h′(x)>0,h(x)在(0,$\frac{1}{2}$)递增,
h(x)<h($\frac{1}{2}$)=2-4ln2,
故a>2-4ln2.
点评 本题考查了切线方程问题,考查函数的单调性、最值问题,考查导数的应用,是一道中档题.

练习册系列答案
 孟建平错题本系列答案
孟建平错题本系列答案 超能学典应用题题卡系列答案
超能学典应用题题卡系列答案
相关题目
5.准线方程为y=4的抛物线的标准方程是( )
| A. | x2=16y | B. | x2=8y | C. | x2=-16y | D. | x2=-8y |
6.若复数z满足$\frac{\overline z}{1+i}=i$,其中i为虚数单位,则z=( )
| A. | 1-i | B. | 1+i | C. | -1-i | D. | -1+i |
3.已知抛物线C:x2=2py(p>0),若直线y=2x,被抛物线所截弦长为4$\sqrt{5}$,则抛物线C的方程为( )
| A. | x2=8y | B. | x2=4y | C. | x2=2y | D. | x2=y |
20.若随机变量X服从正态分布N(μ,σ2)(σ>0),则P(μ-σ<X≤μ+σ)=0.6826,P(μ-2σ<X≤μ+2σ)=0.9544,P(μ-3σ<X≤μ+3σ)=0.9974,已知某随机变量Y近似服从正态分布N(2,σ2),若P(Y>3)=0.1587,则P(Y<0)=( )
| A. | 0.0013 | B. | 0.0228 | C. | 0.1587 | D. | 0.5 |
4.已知抛物线y2=4x,过其焦点F的直线l与抛物线分别交于A、B两点(A在第一象限内),$\stackrel{→}{AF}$=3$\stackrel{→}{FB}$,过AB的中点且垂直于l的直线与x轴交于点G,则三角形ABG的面积为( )
| A. | $\frac{8\sqrt{3}}{9}$ | B. | $\frac{16\sqrt{3}}{9}$ | C. | $\frac{32\sqrt{3}}{9}$ | D. | $\frac{64\sqrt{3}}{9}$ |
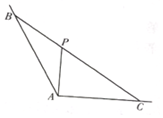 如图,∠BAC=$\frac{2π}{3}$,P为∠BAC内部一点,过点P的直线与∠BAC的两边交于点B,C,且PA⊥AC,AP=$\sqrt{3}$.
如图,∠BAC=$\frac{2π}{3}$,P为∠BAC内部一点,过点P的直线与∠BAC的两边交于点B,C,且PA⊥AC,AP=$\sqrt{3}$.