题目内容

10．已知某组合体的正视图与侧视图相同，如图所示，其中AB=AC，四边形BCDE为矩形，则该组合体的俯视图可以是①②③④（把你认为正确的图的序号都填上）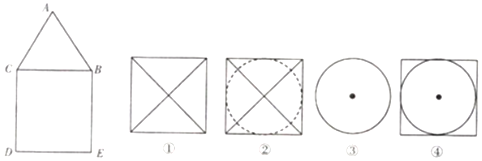

分析 根据几何体的正视图与侧视图相同，得出组合体可以是正四棱柱与正四棱锥的组合体，
也可以是圆柱与正四棱锥的组合体，也可以是圆柱与圆锥的组合体，
也可以是正四棱柱与圆锥的组合体，分四种情况得出对应俯视图．

解答 解：由组合体的正视图与侧视图可知，
该组合体可以是正四棱柱与正四棱锥的组合体，则该组合体的俯视图为①；
该组合体可以是圆柱与正四棱锥的组合体，则该组合体的俯视图为②；
该组合体可以是圆柱与圆锥的组合体，则该组合体的俯视图为③；
该组合体可以是正四棱柱与圆锥的组合体，则该组合体的俯视图为④．
故答案为：①②③④．

点评 本题主要考查了空间组合体的三视图画法问题，也考查了识图能力与空间想象能力，是基础题．

练习册系列答案
相关题目
20．如图，直角梯形ABCD绕底边AD所在直线EF旋转，在旋转前，非直角的腰的端点A可以在DE上选定．当点A选在射线DE上的不同位置时，形成的几何体大小、形状不同，分别画出它的三视图并比较其异同点．
1．设定义域为R的函数f（x）=$\left\{\begin{array}{l}{0}&{x=1}\\{|lg|x-1||}&{x≠1}\end{array}\right.$，则关于x的方程f2（x）+bf（x）+c=0有7个不同实数解的充要条件是（　　）
A．b＜0且c＞0B．b＞0且c＜0C．b＜0且c=0D．b＞0且c=0
18．若两个球的体积之比为1：8，则这两个球的表面积之比为（　　）
A．1：2B．1：4C．1：8D．1：16
5．设M是△ABC边BC上的任意一点，$\overrightarrow{AN}$=$\frac{1}{3}$$\overrightarrow{NM}$，若$\overrightarrow{AN}$=λ$\overrightarrow{AB}$+μ$\overrightarrow{AC}$，则λ+μ=（　　）
A．$\frac{1}{4}$B．$\frac{1}{3}$C．$\frac{1}{2}$D．1
15．已知函数f（x）=（2-a）（x-1）-2lnx，a∈R．
（Ⅰ）若a=1，求曲线y=f（x）在点（1，f（1））处的切线方程；
（Ⅱ）若不等式f（x）＞0在区间（0，$\frac{1}{2}$）上恒成立，求实数a的取值范围．
2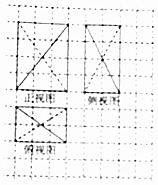．如图，网格纸上小正方形的边长为1，粗线（实线和虚线）为某几何体的三视图，则该几何体外接球的表面积为（　　）
A．24πB．29πC．48πD．58π
19．已知a=sin$\frac{2π}{7}$，b=cos$\frac{2π}{7}$，c=tan$\frac{2π}{7}$，则（　　）
A．b＜a＜cB．c＜b＜aC．b＜c＜aD．a＜b＜c
20．已知实数x，y满足$\left\{\begin{array}{l}{y≥x+2}\\{x+y≤6}\\{x≥1}\end{array}\right.$，则z=2|x-2|+|y|的最小值是（　　）
A．6B．5C．4D．3

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网