题目内容
已知圆O:x2+y2=1,由直线l:x+y+k=0上一点P作圆O的两条切线,切点为A,B,若在直线l上至少存在一点P,使∠APB=60°,则k的取值范围是 .
考点:圆的切线方程
专题:综合题,直线与圆
分析:由题意,∠APB=60°,OP=2,可得P的轨迹方程为x2+y2=4,在直线l上至少存在一点P,使∠APB=60°,可以转化为直线l:x+y+k=0与x2+y2=4至少存在一个交点,利用圆心到直线的距离d=
≤2,即可确定k的取值范围.
| |k| | ||
|
解答:
解:由题意,∠APB=60°,OP=2,
∴P的轨迹方程为x2+y2=4,
∵在直线l上至少存在一点P,使∠APB=60°,
∴直线l:x+y+k=0与x2+y2=4至少存在一个交点,
∴圆心到直线的距离d=
≤2,
∴-2
≤k≤2
,
∴k的取值范围是[-2
,2
].
故答案为:[-2
,2
].
∴P的轨迹方程为x2+y2=4,
∵在直线l上至少存在一点P,使∠APB=60°,
∴直线l:x+y+k=0与x2+y2=4至少存在一个交点,
∴圆心到直线的距离d=
| |k| | ||
|
∴-2
| 2 |
| 2 |
∴k的取值范围是[-2
| 2 |
| 2 |
故答案为:[-2
| 2 |
| 2 |
点评:本题考查直线与圆的位置关系,考查圆的方程,在直线l上至少存在一点P,使∠APB=60°,可以转化为直线l:x+y+k=0与x2+y2=4至少存在一个交点,是解题的关键.

练习册系列答案
相关题目
执行如图所示的程序框图,若输入n的值为7,则输出s的值是( )
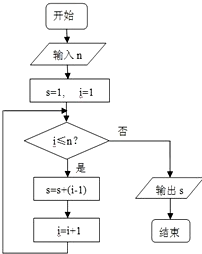

| A、10 | B、16 | C、22 | D、17 |
下列命题中正确的个数是( )
(1)若
为单位向量,且
∥
,|
|=1,则
=
;
(2)若|
|=0,则
=0
(3)若
∥
,则|
|=|
|;
(4)若k
=
,则必有k=0(k∈R);
(5)若k∈R,则k•
=0.
(1)若
| a |
| b |
| a |
| b |
| a |
| b |
(2)若|
| a |
| a |
(3)若
| b |
| a |
| b |
| a |
(4)若k
| a |
| 0 |
(5)若k∈R,则k•
| 0 |
| A、0 | B、1 | C、2 | D、3 |
某流程图如图所示,现输入如下四个函数,则可以输出的函数是( )
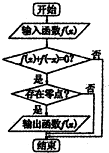

| A、f(x)=x2-1 | ||
B、f(x)=
| ||
C、f(x)=
| ||
| D、f(x)=3sinx+1 |