题目内容
已知直线l:x=my+1过椭圆C:
+
=1 (a>b>0)的右焦点F,抛物线:x2=4
y的焦点为椭圆C的上顶点,且直线l交椭圆C于A、B两点,点A、F、B在直线g:x=3上的射影依次为点D、K、E.
(Ⅰ)求椭圆C的方程;
(Ⅱ)若直线l交y轴于点M,且
=λ1
,
=λ2
.证明:λ1+λ2的值定值;
(Ⅲ)连接AE、BD,直线AE与BD是否相交于定点?若是,请求出定点的坐标,并给予证明;否则,说明理由.
| x2 |
| a2 |
| y2 |
| b2 |
| 2 |
(Ⅰ)求椭圆C的方程;
(Ⅱ)若直线l交y轴于点M,且
| MA |
| AF |
| MB |
| BF |
(Ⅲ)连接AE、BD,直线AE与BD是否相交于定点?若是,请求出定点的坐标,并给予证明;否则,说明理由.
考点:直线与圆锥曲线的综合问题
专题:圆锥曲线中的最值与范围问题
分析:(Ⅰ)由已知条件推导出c=1,b=
,由此能求出椭圆C的方程.
(Ⅱ)由题意知l与y轴交于M(0,-
),设直线l交椭圆于A(x1,y1),B(x2,y2),把直线代入椭圆方程,得到关于y的一元二次方程,利用韦达定理能推导出当m变化时,λ1+λ2的值是定值-3.
(Ⅲ)先探索,当m=0时,AE与BD相交FK的中点NN(2,0),再猜想:当m变化时,AE与BD相交于点N(2,0),然后进行证明.
| 2 |
(Ⅱ)由题意知l与y轴交于M(0,-
| 1 |
| m |
(Ⅲ)先探索,当m=0时,AE与BD相交FK的中点NN(2,0),再猜想:当m变化时,AE与BD相交于点N(2,0),然后进行证明.
解答:
解:(Ⅰ)由题设条件知椭圆右焦点F(1,0),∴c=1,
抛物线x2=4
y的焦点坐标(0,
)…(1分)
∴b=
∴b2=2,
∴a2=b2+c2=3,
∴椭圆C的方程
+
=1.…(3分)
(Ⅱ)由题意知m≠0,且l与y轴交于M(0,-
),
设直线l交椭圆于A(x1,y1),B(x2,y2)
由
⇒(2m2+3)y2+4my-4=0
∴y1+y2=
,y1•y2=
…(5分)
又由
=λ1
∴(x1,y1+
)=λ1(1-x1,-y1),
∴λ1=-1-
,同理λ2=-1-
∴λ1+λ2=-2-
(
+
)…(7分)
∵
+
=
=
•(
)=m…(8分)
∴λ1+λ2=-2-
(
+
)=-2-
•m=-3
所以,当m变化时,λ1+λ2的值是定值,定值为-3.…(9分)
(Ⅲ)先探索,当m=0时,直线l⊥x轴,则ABED为矩形,
由对称性知,AE与BD相交FK的中点N,且N(2,0),
猜想:当m变化时,AE与BD相交于点N(2,0).
证明:由(Ⅱ)知A(x1,y1),B(x2,y2),∴D(3,y1),E(3,y2),
当m变化时,首先证明直线AE过定点N(2,0),
∵lAE:y-y2=
(x-3),
当x=2时,
y=y2+
•(-1)=
=
=0,
∴点N(2,0)在直线lAE上,
同理可证,点N(2,0)也在直线lBD上,
∴当m变化时,AE与BD相交于点N(2,0).
抛物线x2=4
| 2 |
| 2 |
∴b=
| 2 |
∴a2=b2+c2=3,
∴椭圆C的方程
| x2 |
| 3 |
| y2 |
| 2 |
(Ⅱ)由题意知m≠0,且l与y轴交于M(0,-
| 1 |
| m |
设直线l交椭圆于A(x1,y1),B(x2,y2)
由
|
∴y1+y2=
| -4m |
| 2m2+3 |
| -4 |
| 2m2+3 |
又由
| MA |
| AF |
| 1 |
| m |
∴λ1=-1-
| 1 |
| my1 |
| 1 |
| my2 |
∴λ1+λ2=-2-
| 1 |
| m |
| 1 |
| y1 |
| 1 |
| y2 |
∵
| 1 |
| y1 |
| 1 |
| y2 |
| y1+y2 |
| y1y2 |
| -4m |
| 2m2+3 |
| 2m2+3 |
| -4 |
∴λ1+λ2=-2-
| 1 |
| m |
| 1 |
| y1 |
| 1 |
| y2 |
| 1 |
| m |
所以,当m变化时,λ1+λ2的值是定值,定值为-3.…(9分)
(Ⅲ)先探索,当m=0时,直线l⊥x轴,则ABED为矩形,
由对称性知,AE与BD相交FK的中点N,且N(2,0),
猜想:当m变化时,AE与BD相交于点N(2,0).
证明:由(Ⅱ)知A(x1,y1),B(x2,y2),∴D(3,y1),E(3,y2),
当m变化时,首先证明直线AE过定点N(2,0),
∵lAE:y-y2=
| y2-y1 |
| 3-x1 |
当x=2时,
y=y2+
| y2-y1 |
| 3-x1 |
| my1y2-(y1+y2 ) |
| my1-2 |
=
| -4m+4m |
| (my1-2)(2m2-3) |
∴点N(2,0)在直线lAE上,
同理可证,点N(2,0)也在直线lBD上,
∴当m变化时,AE与BD相交于点N(2,0).
点评:本题考查椭圆方程的求法,考查两数和这定值的证明.考查两直线交于定点的探索与证明,解题时要认真审题,注意挖掘题设中的隐含条件,合理地进行等价转化.

练习册系列答案
相关题目
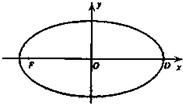 已知在平面直角坐标系xOy中的一个椭圆C,它的中心在原点,左焦点为
已知在平面直角坐标系xOy中的一个椭圆C,它的中心在原点,左焦点为 如图,在圆的内接四边形ABCD中,∠ABC=90°,∠ABD=30°,∠BDC=45°,AD=1,则BC=
如图,在圆的内接四边形ABCD中,∠ABC=90°,∠ABD=30°,∠BDC=45°,AD=1,则BC=