题目内容
10.已知等差数列{an}满足a3=7,a5+a7=26,其前n项和为Sn.(1)求{an}的通项公式及Sn;
(2)令${b_n}=\frac{1}{{{S_n}-n}}(n∈{N^*})$,求数列{bn}的前n项和Tn,并求$\lim_{n→∞}{T_n}$的值.
分析 (1)利用等差数列的通项公式及其前n项和公式即可得出;
(2)利用“裂项求和”方法即可得出.
解答 解:(1)设等差数列{an}的公差为d,
由a5+a7=26,得a6=13,
又a6-a3=3d=6,解得d=2.
所以an=a3+(n-3)d=7+2(n-3)=2n+1.
所以${S_n}=\frac{{{a_1}+{a_n}}}{2}×n=\frac{3+2n+1}{2}×n={n^2}+2n$.
(2)由${b_n}=\frac{1}{{{S_n}-n}}$,得${b_n}=\frac{1}{{{n^2}+n}}=\frac{1}{n(n+1)}=\frac{1}{n}-\frac{1}{n+1}$.
设{bn}的前n项和为Tn,
则${T_n}=({1-\frac{1}{2}})+({\frac{1}{2}-\frac{1}{3}})+({\frac{1}{3}-\frac{1}{4}})+…+({\frac{1}{n}-\frac{1}{n+1}})$=$1-\frac{1}{n+1}$,
$\lim_{n→∞}{T_n}=1$.
点评 本题考查了等差数列的通项公式及其前n项和公式、“裂项求和”方法,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
18.某四棱锥的三视图如图所示,该四棱锥的表面积为( )


| A. | $1+\sqrt{2}$ | B. | 3 | C. | $2+\sqrt{2}$ | D. | 4 |
15.任取一个3位正整数n,则对数log2n是一个正整数的概率为( )
| A. | $\frac{1}{225}$ | B. | $\frac{1}{300}$ | C. | $\frac{1}{450}$ | D. | 以上全不对 |
2.如图,已知PA垂直于平行四边形ABCD所在平面,若PC⊥BD,则平行四边形ABCD一定是( )
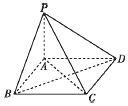

| A. | 正方形 | B. | 菱形 | C. | 矩形 | D. | 非上述三种图形 |
20.解α的终边过点P(4,-3),则cosα的值为( )
| A. | $\frac{4}{5}$ | B. | $-\frac{3}{5}$ | C. | 4 | D. | -3 |