题目内容

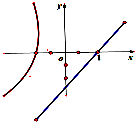
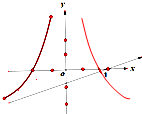
已知椭圆E长轴的一个端点是抛物线y2=12x的焦点，且椭圆焦点与抛物线焦点的距离是1．
（1）求椭圆E的标准方程；
（2）若A、B是椭圆E的左右端点，O为原点，P是椭圆E上异于A、B的任意一点，直线AP、BP分别交y轴于M、N，问
OM
•
0N
是否为定值，说明理由．
考点：直线与圆锥曲线的关系,椭圆的标准方程
专题：向量与圆锥曲线
分析：（1）求出抛物线的焦点坐标，得到椭圆的长半轴长，再由a-c=1求得c，结合隐含条件求得b，则椭圆方程可求；
（2）设出P点坐标，代入椭圆方程，求出直线PA和PB的方程，取x=0求得M，N的坐标，得到向量
OM
，
ON
的坐标，代入数量积公式可得
OM
•
0N
为定值．
解答： 解：（1）由抛物线y2=12x，得焦点为（3，0），
已知可知椭圆的焦点在x轴，且a=3，
又a-c=1，则c=2，
∴b2=a2-c2=5，
故椭圆的方程为：
x2
9
+
y2
5
=1；
（2）设P（x0，y0），则5x02+9y02=45，且A（-3，0），B（3，0），
又直线PA：y=
y0
x0+3
(x+3)，直线PB：y=
y0
x0-3
(x-3)，
令x=0，得：
OM
=(0，
3y0
x0+3
)，
ON
=(0，
-3y0
x0-3
)，
故
OM
•
ON
=
-9y02
x02-9
=
5x02-45
x02-9
=5为定值．
点评：本题考查了椭圆方程的求法，考查了平面向量的数量积运算，是中档题．
练习册系列答案
相关题目
给定集合An={1，2，3，…，n}（n∈N+），映射f：An→An满足：①当i，j∈An，i≠j时，f（i）≠f（j）；②任取m∈An，若m≥2，则有m∈{f（1），f（2），…，f（m）}．则称映射f：An→An是一个“优映射”．例如：用表1表示的映射f：A3→A3是一个“优映射”．
表1                          
i123
 f（i）231
表2
i1234
f（i）3
（1）已知表2表示的映射f：A4→A4是一个“优映射”，请把表2补充完整．
（2）若映射f：A6→A6是“优映射”，且方程f（i）=i的解恰有3个，则这样的“优映射”的个数是
 
．
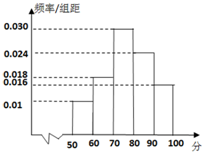某校为了解高一年段期中考试数学科的情况，从高一的所有数学试卷中随机抽取n份试卷进行分析，得到数学成绩频率分布直方图如下图，其中成绩在[70，80）的人数为15，规定：成绩≥80分为优秀．
（Ⅰ）求样本中成绩优秀的试卷份数，并估计该校高一年段期中考试数学成绩的优秀率；
（Ⅱ）从样本成绩在[50，60）和[60，70）这两组中共随机抽取2名同学，求抽取的2名同学中不及格（成绩＜60分）的人数ξ的分布列及数学期望．
三名男生和三名女生站成一排，若男生甲不站在两端，任意两名女生都不相邻，则不同的排列种数是（　　）
A、120B、96C、84D、36
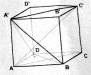在正方体ABCD-A′B′C′D′中，求证：
（1）平面ACC′A′⊥平面A′BD
（2）AC′⊥平面A′BD．
已知点A（2，3），B（1，0），C（-1，0），点D、E分别在线段AB、AC上，
AD
DB
=λ1，
AE
EC
=λ2，且λ1+λ2=1，线段BE、CD交于点P，则点P轨迹的长度是
 
．
已知中心在原点的椭圆C的左焦点F（-
3
，0），右顶点A（2，0）．
（1）求椭圆C的标准方程；
（2）斜率为
1
2
的直线l与椭圆C交于A、B两点，求弦长|AB|的最大值及此时l的直线方程．
已知常数a满足a＞0且a≠1，则函数f（x）=loga（-x），g（x）=ax-a，则他们的图象可能是下列选项（　　）
A、
B、
C、
D、
在△ABC中，A为最小角，B为最大角，已知sin（2A+C）=
4
5
，sinB=
4
5
，求cos2（B+C）

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网