Question

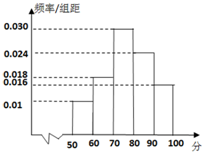某校为了解高一年段期中考试数学科的情况，从高一的所有数学试卷中随机抽取n份试卷进行分析，得到数学成绩频率分布直方图如下图，其中成绩在[70，80）的人数为15，规定：成绩≥80分为优秀．
（Ⅰ）求样本中成绩优秀的试卷份数，并估计该校高一年段期中考试数学成绩的优秀率；
（Ⅱ）从样本成绩在[50，60）和[60，70）这两组中共随机抽取2名同学，求抽取的2名同学中不及格（成绩＜60分）的人数ξ的分布列及数学期望．

Answer 1

考点：离散型随机变量的期望与方差,离散型随机变量及其分布列

专题：计算题,概率与统计

分析：（Ⅰ）由频率分布直方图先求频率，再求样本容量，从而求优秀率；
（Ⅱ）先求两个小组的频数，再求其概率分布，从而求数学期望．

解答： 解：（Ⅰ）由频率分布直方图可得：[70，80）的频率：0.030×10=0.30
所以，n=15÷0.30=50∴第四组[80，90）的频数：0.024×10×50=12；
第五组[90，100]的频数：0.016×10×50=8；
所以，样本中优秀的试卷份数为20，样本的优秀率=

12+8

50

=40%，
∴估计该校高一年段期中考试数学成绩的优秀率为40%；
（Ⅱ）第一组[50，60）的频数：0.01×10×50=5；
第二组[60，70）的频数：0.018×10×50=9；ξ的所有可能取值为0，1，2．
依题意，得P(ξ=0)=

C 2 9

C 2 14

=

36

91

，P(ξ=1)=

C 1 5 C 1 9

C 2 14

=

45

91

，P(ξ=2)=

C 2 5

C 2 14

=

10

91

．
∴ξ的分布列为：

ξ	0	1	2
P	36 91	45 91	10 91

∴Eξ=0×

36

91

+1×

45

91

+2×

10

91

=

65

91

．

点评：本题考查了概率分布与数学期望，同时考查了频率分布直方图的应用，属于中档题．