题目内容
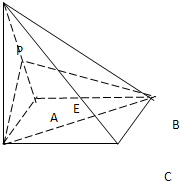 已知四棱锥P-ABCD中,PD⊥平面ABCD,ABCD是正方形,E是PA的中点,
已知四棱锥P-ABCD中,PD⊥平面ABCD,ABCD是正方形,E是PA的中点,(1)若PD=AD,求PC与面AC所成的角
(2)求证:PC∥平面EBD
(3)求证:平面PBC⊥平面PCD.
考点:平面与平面垂直的判定,直线与平面平行的判定,直线与平面垂直的判定
专题:综合题,空间位置关系与距离,空间角
分析:(1)由PD⊥平面ABCD,可得∠PCD是PC与面AC所成的角;
(2)连BD,与AC交于O,利用三角形的中位线,可得线线平行,从而可得线面平行;
(3)证明BC⊥平面PCD,即可证得平面PBC⊥平面PCD.
(2)连BD,与AC交于O,利用三角形的中位线,可得线线平行,从而可得线面平行;
(3)证明BC⊥平面PCD,即可证得平面PBC⊥平面PCD.
解答:
 (1)解:∵PD⊥平面ABCD,
(1)解:∵PD⊥平面ABCD,
∴∠PCD是PC与面AC所成的角
∵ABCD是正方形,PD=AD,
∴∠PCD=45°;
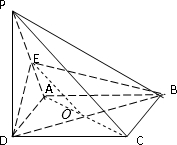
(2)证明:连BD,与AC交于O,连接EO
∵ABCD是正方形,∴O是AC的中点,
∵E是PA的中点,
∴EO∥PC
又∵EO?平面EBD,PC?平面EBD
∴PC∥平面EBD;
(3)∵PD⊥平面ABCD,BC?平面ABCD
∴BC⊥PD
∵ABCD是正方形,∴BC⊥CD
又∵PD∩CD=D
∴BC⊥平面PCD
∵BC?平面PBC
∴平面PBC⊥平面PCD.
 (1)解:∵PD⊥平面ABCD,
(1)解:∵PD⊥平面ABCD,∴∠PCD是PC与面AC所成的角
∵ABCD是正方形,PD=AD,
∴∠PCD=45°;
(2)证明:连BD,与AC交于O,连接EO
∵ABCD是正方形,∴O是AC的中点,
∵E是PA的中点,
∴EO∥PC
又∵EO?平面EBD,PC?平面EBD
∴PC∥平面EBD;
(3)∵PD⊥平面ABCD,BC?平面ABCD
∴BC⊥PD
∵ABCD是正方形,∴BC⊥CD
又∵PD∩CD=D
∴BC⊥平面PCD
∵BC?平面PBC
∴平面PBC⊥平面PCD.
点评:本题考查线面角、线面平行,考查面面垂直,掌握线面平行,面面垂直的判定方法是关键.

练习册系列答案
相关题目
在△ABC中,∠A、∠B、∠C所对的边长分别是4、
,2则cosA的值为( )
| 7 |
A、-
| ||||
B、
| ||||
C、-
| ||||
D、
|
正方体ABCD-A1B1C1D1中,O为侧面BCC1B1的中心,则AO与平面ABCD所成的角的正弦值为( )
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
 某市为响应国家节能减排建设的号召,唤起人们从自己身边的小事做起,开展了以“再小的力量也是一种支持”为主题的宣传教育活动,其中有两则公益广告:
某市为响应国家节能减排建设的号召,唤起人们从自己身边的小事做起,开展了以“再小的力量也是一种支持”为主题的宣传教育活动,其中有两则公益广告: 如图,在Rt△ABC中,已知BC=5,AB=3,AC=4,若长为10的线段PQ以点A为中点,问
如图,在Rt△ABC中,已知BC=5,AB=3,AC=4,若长为10的线段PQ以点A为中点,问