题目内容
已知数列{an}的前n项和是Sn,且Sn=2an-n(n∈N*).
(1)证明:数列{an+1}是等比数列,并求数列{an}的通项公式;
(2)记bn=
,求数列{bn}的前n项和.
(1)证明:数列{an+1}是等比数列,并求数列{an}的通项公式;
(2)记bn=
| an+1 |
| anan+1 |
考点:数列的求和
专题:等差数列与等比数列
分析:(1)由已知条件推导出an=2an-1+1,由此能证明数列{an+1}是首项为2,公比为2的等比数列,从而能求出an=2n-1.
(2)bn=
=
=
-
,由此利用裂项求和法能求出数列{bn}的前n项和.
(2)bn=
| an+1 |
| anan+1 |
| 2n |
| (2n-1)(2n+1-1) |
| 1 |
| 2n-1 |
| 1 |
| 2n+1-1 |
解答:
解:(1)∵Sn=2an-n,
∴n=1时,a1=2a1-1,解得a1=1.
n≥2时,an=Sn-Sn-1=(2an-n)-(2an-1-n+1)
=2an-2an-1-1,
∴an=2an-1+1,
∴an+1=2(an-1+1),
∵a1+1=2,
∴数列{an+1}是首项为2,公比为2的等比数列.
∴an+1=2n,
∴an=2n-1.
(2)∵bn=
=
=
-
,
∴数列{bn}的前n项和:
Sn=
-
+
-
+
-
=1-
=
.
∴数列{bn}的前n项和为
.
∴n=1时,a1=2a1-1,解得a1=1.
n≥2时,an=Sn-Sn-1=(2an-n)-(2an-1-n+1)
=2an-2an-1-1,
∴an=2an-1+1,
∴an+1=2(an-1+1),
∵a1+1=2,
∴数列{an+1}是首项为2,公比为2的等比数列.
∴an+1=2n,
∴an=2n-1.
(2)∵bn=
| an+1 |
| anan+1 |
| 2n |
| (2n-1)(2n+1-1) |
| 1 |
| 2n-1 |
| 1 |
| 2n+1-1 |
∴数列{bn}的前n项和:
Sn=
| 1 |
| 2-1 |
| 1 |
| 22-1 |
| 1 |
| 22-1 |
| 1 |
| 23-1 |
| 1 |
| 2n-1 |
| 1 |
| 2n+1-1 |
=1-
| 1 |
| 2n+1-1 |
=
| 2n+1-2 |
| 2n+1-1 |
∴数列{bn}的前n项和为
| 2n+1-2 |
| 2n+1-1 |
点评:本题考等比数列的证明,考查数列的通项公式和前n项和公式的求法,注意裂项求和法的合理运用.

练习册系列答案
相关题目
圆心(1,-4),且过点(4,0)的圆的标准方程为( )
| A、(x-1)2+(y+4)2=25 |
| B、(x+1)2+(y-4)2=25 |
| C、(x-1)2+(y+4)2=5 |
| D、(x+1)2+(y-4)2=5 |
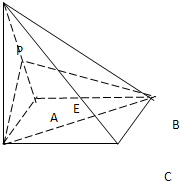 已知四棱锥P-ABCD中,PD⊥平面ABCD,ABCD是正方形,E是PA的中点,
已知四棱锥P-ABCD中,PD⊥平面ABCD,ABCD是正方形,E是PA的中点, (1)已知角a的终边经过点P(3,-4)求:
(1)已知角a的终边经过点P(3,-4)求: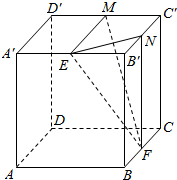 在正方体ABCD-A′B′C′D′中,E,F,M,N分别是A′B′,BC,C′D′,B′C′的中点.
在正方体ABCD-A′B′C′D′中,E,F,M,N分别是A′B′,BC,C′D′,B′C′的中点.