题目内容
在△ABC中，∠A、∠B、∠C所对的边长分别是4、
，2则cosA的值为（ ）
| 7 |
A、-
| ||||
B、
| ||||
C、-
| ||||
D、
|
考点：余弦定理
专题：解三角形
分析：由条件利用余弦定理求得cosA=
的值．
| b2+c2-a2 |
| 2bc |
解答：
解：在△ABC中，∵∠A、∠B、∠C所对的边长分别是4、
，2，
则由余弦定理可得 cosA=
=
=-
，
故选：C．
| 7 |
则由余弦定理可得 cosA=
| b2+c2-a2 |
| 2bc |
| 7+4-16 | ||
2×
|
5
| ||
| 28 |
故选：C．
点评：本题主要考查余弦定理的应用，属于基础题．
练习册系列答案
相关题目
如果等差数列{an}中，a4+a6=8，那么数列{an}的前9项和为（ ）
| A、27 | B、36 | C、54 | D、72 |
正四棱锥P-ABCD的底面边长是2，侧棱长是
，且它的五个顶点都在同一个球面上，则此球的半径是（ ）
| 6 |
| A、1 | ||
| B、2 | ||
C、
| ||
| D、3 |
下列函数中，满足“对?x1，x2∈（0，+∞），当x1＜x2，都有f（x1）＞f（x2）”的是（ ）
| A、f（x）=x2 | ||
| B、f（x）=lnx | ||
| C、f（x）=-|x+2| | ||
D、f（x）=(
|
用辗转相除法求108和45的最大公约数为（ ）
| A、2 | B、9 | C、18 | D、27 |
过点P（3，-2），且垂直于直线3x+2y-8=0的直线方程为（ ）
| A、3x+2y-5=0 |
| B、3x+2y+5=0 |
| C、2x-3y-12=0 |
| D、2x-3y+12=0 |
圆心（1，-4），且过点（4，0）的圆的标准方程为（ ）
| A、（x-1）2+（y+4）2=25 |
| B、（x+1）2+（y-4）2=25 |
| C、（x-1）2+（y+4）2=5 |
| D、（x+1）2+（y-4）2=5 |
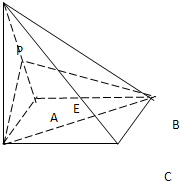已知四棱锥P-ABCD中，PD⊥平面ABCD，ABCD是正方形，E是PA的中点，