题目内容
如图，在Rt△ABC中，已知BC=5，AB=3，AC=4，若长为10的线段PQ以点A为中点，问| PQ |
| BC |
| BP |
| CQ |
考点：平面向量数量积的运算
专题：平面向量及应用
分析：如图所示，建立直角坐标系．B（3，0），C（0，4）．设P（5cosα，5sinα），Q（-5cosα，-5sinα），α∈[0，2π）．利用数量积的坐标运算可得
•
=-25(
sinα-
cosα)-25=-25sin（α-φ）-25≤-25×（-1）-25=0，其中sinφ=
，cosφ=
．联立
，解得即可得出．
| BP |
| CQ |
| 4 |
| 5 |
| 3 |
| 5 |
| 3 |
| 5 |
| 4 |
| 5 |
|
解答：
解：如图所示，建立直角坐标系．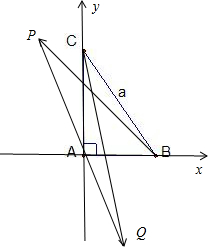
B（3，0），C（0，4）．
设P（5cosα，5sinα），则Q（-5cosα，-5sinα），α∈[0，2π）．
∴
•
=（5cosα-3，5sinα）•（-5cosα，-5sinα-4）
=-5cosα（5cosα-3）-5sinα（5sinα+4）
=-25cos2α+15cosα-25sin2α-20sinα
=-25(
sinα-
cosα)-25
=-25sin（α-φ）-25≤-25×（-1）-25=0，其中sinφ=
，cosφ=
．
由
，解得
此时，
=（-6，8），
=（-3，4）．
∵
=2
，∴此时
∥
，因此
与
的夹角θ=0．
∴
与
的夹角θ取0时，
•
的值最大为0．
B（3，0），C（0，4）．
设P（5cosα，5sinα），则Q（-5cosα，-5sinα），α∈[0，2π）．
∴
| BP |
| CQ |
=-5cosα（5cosα-3）-5sinα（5sinα+4）
=-25cos2α+15cosα-25sin2α-20sinα
=-25(
| 4 |
| 5 |
| 3 |
| 5 |
=-25sin（α-φ）-25≤-25×（-1）-25=0，其中sinφ=
| 3 |
| 5 |
| 4 |
| 5 |
由
|
|
此时，
| PQ |
| BC |
∵
| PQ |
| BC |
| PQ |
| BC |
| PQ |
| BC |
∴
| PQ |
| BC |
| BP |
| CQ |
点评：本题考查了向量数量积的坐标运算、三角函数的单调性有界性、同角三角函数的基本关系式、向量共线等基础知识与基本技能方法，考查了推理能力和计算能力，属于难题．
练习册系列答案
华东师大版一课一练系列答案
孟建平名校考卷系列答案
相关题目
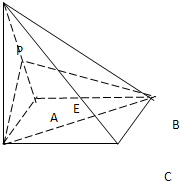已知四棱锥P-ABCD中，PD⊥平面ABCD，ABCD是正方形，E是PA的中点，
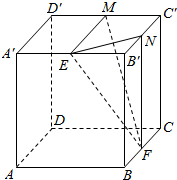在正方体ABCD-A′B′C′D′中，E，F，M，N分别是A′B′，BC，C′D′，B′C′的中点．
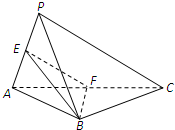如图，在三棱锥P-ABC中，平面ABC⊥平面PAC，AB=BC，E，F分别是PA，AC的中点．求证：