题目内容
正方体ABCD-A1B1C1D1中,O为侧面BCC1B1的中心,则AO与平面ABCD所成的角的正弦值为( )
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
考点:直线与平面所成的角
专题:计算题,空间角
分析:取BC中点E,连接OE,AE,则OE⊥平面ABCD,可得∠OAE为AO与平面ABCD所成的角,即可得出结论.
解答:
 解:取BC中点E,连接OE,AE,则OE⊥平面ABCD,
解:取BC中点E,连接OE,AE,则OE⊥平面ABCD,
∴∠OAE为AO与平面ABCD所成的角,
设正方体的棱长为2,则OE=1,AE=
,OA=
,
∴AO与平面ABCD所成的角的正弦值为
=
.
故选:D.
 解:取BC中点E,连接OE,AE,则OE⊥平面ABCD,
解:取BC中点E,连接OE,AE,则OE⊥平面ABCD,∴∠OAE为AO与平面ABCD所成的角,
设正方体的棱长为2,则OE=1,AE=
| 5 |
| 6 |
∴AO与平面ABCD所成的角的正弦值为
| 1 | ||
|
| ||
| 6 |
故选:D.
点评:本题考查直线与平面所成的角,考查学生的计算能力,作出直线与平面所成的角是关键.

练习册系列答案
相关题目
如果等差数列{an}中,a4+a6=8,那么数列{an}的前9项和为( )
| A、27 | B、36 | C、54 | D、72 |
过点P(3,-2),且垂直于直线3x+2y-8=0的直线方程为( )
| A、3x+2y-5=0 |
| B、3x+2y+5=0 |
| C、2x-3y-12=0 |
| D、2x-3y+12=0 |
圆心(1,-4),且过点(4,0)的圆的标准方程为( )
| A、(x-1)2+(y+4)2=25 |
| B、(x+1)2+(y-4)2=25 |
| C、(x-1)2+(y+4)2=5 |
| D、(x+1)2+(y-4)2=5 |
已知函数f(x)=
x3-x2+ax+b,其中a<0,如果存在实数t,使f′(t)<0,则f′(2-t)•f′(
)的值( )
| 1 |
| 3 |
| 3t+1 |
| 4 |
| A、必为正数 | B、必为负数 |
| C、必为非负 | D、必为非正 |
已知非零向量是
,
,
满足
+
+
=
,(|
|•
-|
|•
)•
=0,且2(
•
)=|
|•|
|,则由向量
,
,
构成的三角形的三个内角分别为( )
| a |
| b |
| c |
| a |
| b |
| c |
| 0 |
| b |
| a |
| a |
| b |
| c |
| a |
| b |
| a |
| b |
| a |
| b |
| c |
| A、30°,60°,90° |
| B、45°,45°,90° |
| C、30°,30°,120° |
| D、60°,60°,60° |
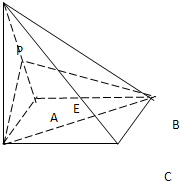 已知四棱锥P-ABCD中,PD⊥平面ABCD,ABCD是正方形,E是PA的中点,
已知四棱锥P-ABCD中,PD⊥平面ABCD,ABCD是正方形,E是PA的中点,