题目内容
已知函数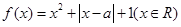 .
.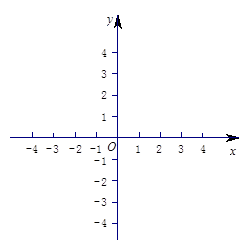
(1)画出 a =" 0" 时函数 的图象;
的图象;
(2)求函数 的最小值.
的最小值.
(1)函数的图像的求解,对于二次函数的图像作对称变换可知道。
(2)当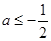 时,函数
时,函数 的最小值为
的最小值为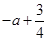
当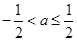 时,函数
时,函数 的最小值为
的最小值为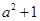
当a >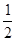 时,函数f (x)的最小值为
时,函数f (x)的最小值为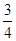 +a
+a
解析试题分析:解:(1)略 4分
(2)①当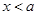 时,
时,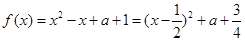 5分
5分
若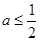 ,则函数
,则函数 在
在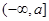 上单调递减,从而函数
上单调递减,从而函数 在
在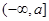 上的最小值为
上的最小值为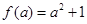
若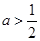 ,则函数
,则函数 在
在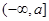 上的最小值为
上的最小值为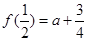 7分
7分
②当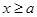 时,
时,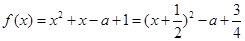 8分
8分
若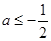 ,则函数
,则函数 在
在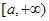 上的最小值为
上的最小值为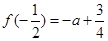
若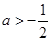 ,则函数
,则函数 在
在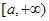 上的最小值为
上的最小值为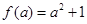 10分
10分
综上,当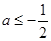 时,函数
时,函数 的最小值为
的最小值为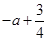
当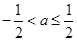 时,函数
时,函数 的最小值为
的最小值为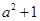
当a >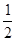 时,函数f (x)的最小值为
时,函数f (x)的最小值为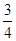 +a. 12分
+a. 12分
考点:函数的图像与值域
点评:解决的关键是对于绝对值函数的理解,要去掉绝对值符号,然后结合二次函数的性质来得到图像以及相应的值域,属于基础题。

练习册系列答案
 鸿图图书寒假作业假期作业吉林大学出版社系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案
相关题目
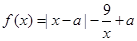 ,
,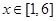 ,
,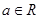 .
.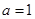 ,试判断并证明函数
,试判断并证明函数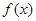 的单调性;
的单调性;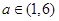 时,求函数
时,求函数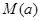 .
. ,
,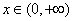 ,是否存在实数
,是否存在实数 ,使
,使 同时满足下列两个条件:(1)
同时满足下列两个条件:(1) 上是减函数,在
上是减函数,在 上是增函数;(2)
上是增函数;(2) ,若存在,求出
,若存在,求出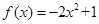 是偶函数,且在
是偶函数,且在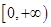 上是减少的。(13分)
上是减少的。(13分)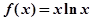 ,
,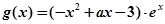 (其中
(其中 实数,
实数,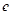 是自然对数的底数).
是自然对数的底数).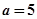 时,求函数
时,求函数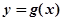 在点
在点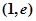 处的切线方程;
处的切线方程; 在区间
在区间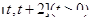 上的最小值;
上的最小值;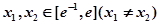 ,使方程
,使方程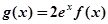 成立,求实数
成立,求实数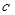 的取值范围.
的取值范围. (a>0,且a≠1),
(a>0,且a≠1), =
= .
. 的图象恒过定点A,求A点坐标;
的图象恒过定点A,求A点坐标; 的图像过点(2,
的图像过点(2, ),证明:函数
),证明:函数 在
在 (1,2)上有唯一的零点.
(1,2)上有唯一的零点.  (
( ≠0)在区间(-1,1)上的单调性。
≠0)在区间(-1,1)上的单调性。 ,总有
,总有 ;②
;② ;③若
;③若 ,则有
,则有 成立.
成立.  的值;(2) 函数
的值;(2) 函数 在区间[0,1]上是否同时适合①②③?并予以证明
在区间[0,1]上是否同时适合①②③?并予以证明 ,使得
,使得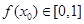 ,且
,且 ,求证:
,求证: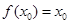
 ,
, .其中
.其中 表示不超过
表示不超过 的最大整数,例如
的最大整数,例如 .
. 的奇偶性,并说明理由;
的奇偶性,并说明理由;