题目内容
已知
,
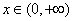，是否存在实数
,使
同时满足下列两个条件：（1）在
上是减函数，在
上是增函数；（2）的最小值是
，若存在，求出，若不存在，说明理由.
解析试题分析：设
∵在上是减函数，在
上是增函数
∴
在上是减函数，在上是增函数.
∴
∴
解得
经检验，时，满足题设的两个条件.
考点：本题考查了对数函数的单调性
点评：此类问题常常利用函数的单调性列出关于自变量的式子处理，属基础题
练习册系列答案
相关题目
题目内容
已知,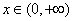，是否存在实数,使同时满足下列两个条件：（1）在上是减函数，在上是增函数；（2）的最小值是，若存在，求出，若不存在，说明理由.
解析试题分析：设
∵在上是减函数，在上是增函数
∴在上是减函数，在上是增函数.
∴ ∴ 解得
经检验，时，满足题设的两个条件.
考点：本题考查了对数函数的单调性
点评：此类问题常常利用函数的单调性列出关于自变量的式子处理，属基础题
．
，求曲线
在点
处的切线方程；
的单调区间；
．若至少存在一个
，使得
成立，求实数
的取值范围．
=
恒成立，求实数a的取值范围．
且
，当
时，恒有
的解析式；
的解集为空集，求
的范围。
和
，使得函数
和
对其定义域上的任意实数
分别满足：
和
，则称直线
为
，
为自然对数的底数)．
的极值；
和
是否存在隔离直线？若存在，求出此隔离直线方程；若不存在，请说明理由．
时，求函数在
上的最大值和最小值；
在
处取得极值，不等式
对
恒成立，求实数
的取值范围。
是R上的奇函数，且当
时，
，求
.
的图象；
.
的解集；
对