题目内容
证明:函数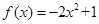 是偶函数,且在
是偶函数,且在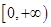 上是减少的。(13分)
上是减少的。(13分)
直接用定义证明函数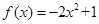 的奇偶性和单调性。
的奇偶性和单调性。
解析试题分析:证明:函数 的定义域为
的定义域为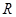 ,对于任意的
,对于任意的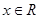 ,都有
,都有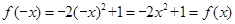 ,∴
,∴ 是偶函数.
是偶函数.
(Ⅱ)证明:在区间 上任取
上任取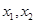 ,且
,且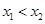 ,则有
,则有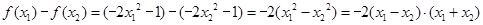 ,
,
∵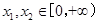 ,
,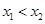 ,∴
,∴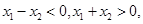
即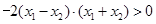
∴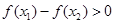 ,即
,即 在
在 上是减少的.
上是减少的.
考点:函数的奇偶性;函数的单调性。
点评:用定义法证明函数单调性的步骤:一设二作差三变形四判断符号五得出结论,其中最重要的是四变形,最好变成几个因式乘积的形式,这样便于判断符号。

练习册系列答案
 53随堂测系列答案
53随堂测系列答案
相关题目
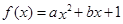 在
在 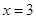 处的切线方程为
处的切线方程为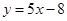 .
.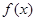 的解析式;
的解析式;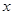 的方程
的方程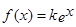 恰有两个不同的实根,求实数
恰有两个不同的实根,求实数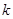 的值 ;
的值 ;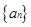 满足
满足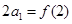 ,
,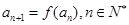 ,求
,求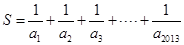 的整数部分.
的整数部分. 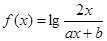 且
且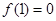 ,当
,当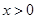 时,恒有
时,恒有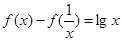
 的解析式;
的解析式;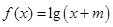 的解集为空集,求
的解集为空集,求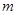 的范围。
的范围。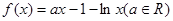
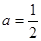 时,求函数在
时,求函数在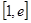 上的最大值和最小值;
上的最大值和最小值;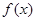 在
在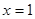 处取得极值,不等式
处取得极值,不等式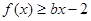 对
对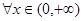 恒成立,求实数
恒成立,求实数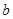 的取值范围。
的取值范围。 是R上的奇函数,且当
是R上的奇函数,且当 时,
时, ,求
,求 .
.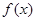 为定义域上的单调函数,求实数m的取值范围;
为定义域上的单调函数,求实数m的取值范围;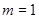 ,
,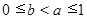 时,证明:
时,证明: .
.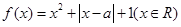 .
.
 的图象;
的图象;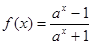 (a>1).
(a>1).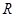 的函数
的函数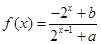 是奇函数。
是奇函数。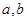 的值;
的值;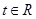 ,不等式
,不等式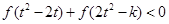 恒成立,求
恒成立,求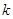 的取值范围;
的取值范围;