题目内容
已知定义域为[0,1]的函数同时满足以下三个条件:①对任意 ,总有
,总有 ;②
;② ;③若
;③若 ,则有
,则有 成立.
成立.
(1) 求 的值;(2) 函数
的值;(2) 函数 在区间[0,1]上是否同时适合①②③?并予以证明
在区间[0,1]上是否同时适合①②③?并予以证明
(3) 假定存在 ,使得
,使得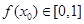 ,且
,且 ,求证:
,求证: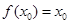
(1)  (2) 函数
(2) 函数 在区间[0,1]上同时适合①②③.
在区间[0,1]上同时适合①②③.
(3)运用反证法思想来证明不等式的成立性。假设不成立,则可知 来证明。
来证明。
解析试题分析:(1)解:由①知: ;由③知:
;由③知: ,即
,即 ;
;
∴
(2 ) 证明:由题设知: ;
;
由 知
知 ,得
,得 ,有
,有 ;
;
设 ,则
,则 ,
, ;
;
∴
即
∴函数 在区间[0,1]上同时适合①②③.
在区间[0,1]上同时适合①②③.
(3) 证明:若 ,则由题设知:
,则由题设知: ,且由①知
,且由①知 ,
,
∴由题设及③知:
矛盾;
若 ,则则由题设知:
,则则由题设知: ,且由①知
,且由①知 ,
,
∴同理得: ,矛盾;故由上述知:
,矛盾;故由上述知: 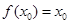
考点:函数恒成立问题
点评:本题考查函数值的求法和函数恒成立问题的应用,解题时要认真审题,仔细解答

练习册系列答案
相关题目
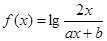 且
且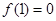 ,当
,当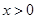 时,恒有
时,恒有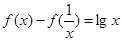
 的解析式;
的解析式;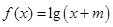 的解集为空集,求
的解集为空集,求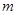 的范围。
的范围。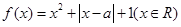 .
.
 的图象;
的图象;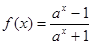 (a>1).
(a>1). 有意义的(x,y)出现的概率;
有意义的(x,y)出现的概率;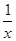 在(0,1)上是减函数.
在(0,1)上是减函数.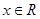 .
.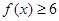 的解集;
的解集;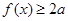 对
对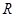 的函数
的函数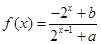 是奇函数。
是奇函数。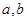 的值;
的值;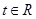 ,不等式
,不等式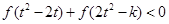 恒成立,求
恒成立,求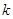 的取值范围;
的取值范围;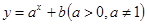 的图象过
的图象过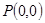 与
与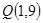 两点,设函数
两点,设函数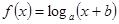 ;
;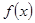 的定义域;
的定义域; 的值域,判断g(x)奇偶性,并说明理由.
的值域,判断g(x)奇偶性,并说明理由.