题目内容
已知函数 (a>0,且a≠1),
(a>0,且a≠1), =
= .
.
(1)函数 的图象恒过定点A,求A点坐标;
的图象恒过定点A,求A点坐标;
(2)若函数 的图像过点(2,
的图像过点(2, ),证明:函数
),证明:函数 在
在 (1,2)上有唯一的零点.
(1,2)上有唯一的零点.
(1)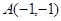
(2)先利用已知条件求出a,在利用单调性和零点存在定理即可证明
解析试题分析:(1)因为对数函数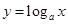 恒过顶点(1,0),
恒过顶点(1,0),
所以令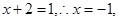 所以过顶点
所以过顶点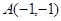 5分
5分
(2)∵
∴代入计算可得a=2 7分
∴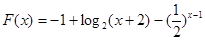
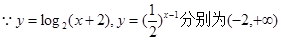 上的增函数和减函数
上的增函数和减函数
∴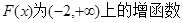
∴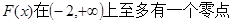 10分
10分
又(1,2)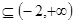
∴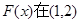 上至多有一个零点. 12分
上至多有一个零点. 12分
而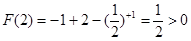
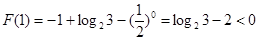
∴函数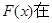 (1,2)
(1,2)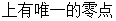 16分
16分
考点:本小题主要考查对数函数过定点和函数的单调性以及零点存在定理的应用.
点评:指数函数和对数函数都过定点,这条性质要灵活应用;利用函数的零点存在定理时要注意它只能判断有零点,不能判断零点的个数.

练习册系列答案
相关题目
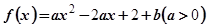 在区间
在区间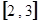 上的值域为
上的值域为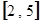
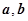 的值;
的值;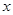 的函数
的函数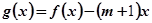 在区间
在区间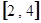 上为单调函数,求实数
上为单调函数,求实数 的取值范围.
的取值范围. 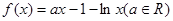
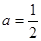 时,求函数在
时,求函数在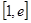 上的最大值和最小值;
上的最大值和最小值;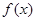 在
在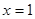 处取得极值,不等式
处取得极值,不等式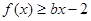 对
对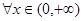 恒成立,求实数
恒成立,求实数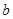 的取值范围。
的取值范围。 .
.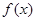 为定义域上的单调函数,求实数m的取值范围;
为定义域上的单调函数,求实数m的取值范围;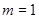 ,
,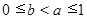 时,证明:
时,证明: .
.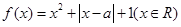 .
.
 的图象;
的图象;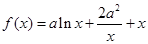 .
. 在点
在点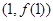 处的切线与直线
处的切线与直线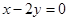 垂直,求实数
垂直,求实数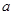 的值.
的值.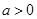 ,求
,求 的最小值
的最小值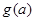 ;
;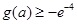 .
.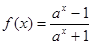 (a>1).
(a>1).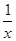 在(0,1)上是减函数.
在(0,1)上是减函数. 。
。