题目内容

某工厂生产A、B、C三种不同型号的产品，产品的数量之比依次为2：3：5，现用分层抽样的方法抽出样本容量为80的样本，那么应当从A型产品中抽出的件数为（　　）
A、16B、24C、40D、160
考点：分层抽样方法
专题：概率与统计
分析：由分层抽样方法的特征是各层所抽取的样本比例数相等，求出答案即可．
解答： 解：根据分层抽样方法的特征，各层所抽取的样本数比例应相等，
∴应从A型产品中抽出的件数为80×
2
2+3+5
=16．
故选：A．
点评：本题考查了分层抽样的应用问题，解题时应熟悉分层抽样方法的特征是什么，是容易题．
练习册系列答案
相关题目
若向量
a
≠
e
，|
e
|=1，对任意的t∈R，|
a
-t
e
|≥|
a
-
e
|成立，则
a
•
e
=（　　）
A、0
B、1
C、-1
D、
0
若函数f（x）=2sin（ωx+φ）的部分图象如图所示，则ω和φ的取值是（　　）
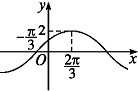
A、ω=
1
2
，φ=-
π
6
B、ω=
1
2
，φ=
π
6
C、ω=1，φ=-
π
3
D、ω=1，φ=
π
3
已知数列{an}共有2n+1项，其中奇数项通项公式为an=2n-1，则数列{an}的奇数项的和为（　　）
A、2（2n+1-1）-n-1
B、
2
3
（4n+1-1）-n-1
C、2（4n+1-1）-n-1
D、
2
3
（2n+1-1）-n-1
已知椭圆准线x=4对应焦点（2，0），离心率e=
1
2
，则椭圆方程为（　　）
A、
x2
8
+
y2
4
=1
B、3x2+y2+28y+60=0
C、3x2+4y2-8x=0
D、2x2+3y2-7x+4=0
在直角坐标系xOy中，直线l的参数方程为
x=t
y=t+4
（t为参数）．曲线C的参数方程为
x=2+2
2
cosθ
y=2+2
2
sinθ
（θ为参数），则直线l和曲线C的公共点有（　　）
A、0个B、1个C、2个D、无数个
集合{a，b，c，d}的子集有（　　）
A、4个B、8个
C、16个D、32个
若某程序框图如图所示，当输入50时，则该程序运算后输出的结果是（　　）
A、8B、6C、4D、2
已知向量
a
=（sinx，1），
b
=（cosx，1），x∈R．
（1）当x=
π
4
时，求向量a+b的坐标；
（2）若函数f（x）=|
a
+
b
|2+m为奇函数，求实数m的值．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网