题目内容
已知向量
=(sinx,1),
=(cosx,1),x∈R.
(1)当x=
时,求向量a+b的坐标;
(2)若函数f(x)=|
+
|2+m为奇函数,求实数m的值.
| a |
| b |
(1)当x=
| π |
| 4 |
(2)若函数f(x)=|
| a |
| b |
考点:平面向量数量积的运算,函数奇偶性的性质
专题:平面向量及应用
分析:(1)当x=
时,向量
=
=(
,1).
(2)由于
+
=(sinx+cosx,2),可得f(x)=(sinx+cosx)2+4+m=sin2x+5+m.由于函数f(x)为奇函数,可得f(-π)=-f(π).化简即可得出.
| π |
| 4 |
| a |
| b |
| ||
| 2 |
(2)由于
| a |
| b |
解答:
解:(1)当x=
时,向量
+
=(
,1)+(
,1)=(
,2).
(2)∵
+
=(sinx+cosx,2),
∴f(x)=(sinx+cosx)2+4+m=sin2x+5+m.
∵函数f(x)为奇函数,∴f(-π)=-f(π).
∴sin(-2π)+5+m=-(sin2π+5+m),
化为5+m=0,解得m=-5.
| π |
| 4 |
| a |
| b |
| ||
| 2 |
| ||
| 2 |
| 2 |
(2)∵
| a |
| b |
∴f(x)=(sinx+cosx)2+4+m=sin2x+5+m.
∵函数f(x)为奇函数,∴f(-π)=-f(π).
∴sin(-2π)+5+m=-(sin2π+5+m),
化为5+m=0,解得m=-5.
点评:本题考查了向量的坐标运算、数量积性质、奇偶性,考查了计算能力,属于中档题.

练习册系列答案
 考前必练系列答案
考前必练系列答案
相关题目
下列函数中周期为π且图象关于直线x=
对称的函数是( )
| π |
| 6 |
A、y=2sin(2x-
| ||||
B、y=2sin(
| ||||
C、y=2sin(2x+
| ||||
D、y=2sin(
|
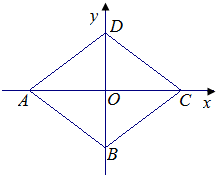 如图,在平面直角坐标系中,菱形ABCD的两个顶点C,D的坐标分别为(4,0),(0,3).现有两动点P,Q分别从A,C同时出发,点P沿线段AD以每秒1个单位的速度向终点D运动,点Q沿折线CBA以每秒2个单位的速度向终点A运动,设运动时间为t秒.
如图,在平面直角坐标系中,菱形ABCD的两个顶点C,D的坐标分别为(4,0),(0,3).现有两动点P,Q分别从A,C同时出发,点P沿线段AD以每秒1个单位的速度向终点D运动,点Q沿折线CBA以每秒2个单位的速度向终点A运动,设运动时间为t秒.