题目内容
已知sinα=
+cosα,且α∈(0,
),求
的值.
| 1 |
| 2 |
| π |
| 2 |
| cos2α | ||
sin(α-
|
考点:二倍角的余弦,两角和与差的正弦函数
专题:三角函数的求值
分析:由条件求得sin2α的值,进而求得sin α+cosα的值,花简要求的式子为-
(sinα+cosα),从而得到答案.
| 2 |
解答:
解:由题意知sin α-cosα=
,两边平方可得sin2α=
,
所以(sin α+cos α)2=1+sin2α=
,
又α∈(0,
),所以sin α+cosα=
.
=
=-
(sinα+cosα)=-
.
| 1 |
| 2 |
| 3 |
| 4 |
所以(sin α+cos α)2=1+sin2α=
| 7 |
| 4 |
又α∈(0,
| π |
| 2 |
| ||
| 2 |
| cos2α | ||
sin(α-
|
| cos2α-sin2α | ||||
|
| 2 |
| ||
| 2 |
点评:本题主要考查两角和的正弦公式,二倍角公式的应用,属于基础题.

练习册系列答案
 通城学典默写能手系列答案
通城学典默写能手系列答案
相关题目
已知实数a,b满足a+b>0,b<0,则a,b,-a,-b的大小关系是( )
| A、a>-b>b>-a |
| B、a>b>-b>-a |
| C、a>-b>-a>b |
| D、a>b>-a>-b |
 已知:正方形ABCD与正方形ABEF不共面,N、M分别在AE和BD上,AN=DM.
已知:正方形ABCD与正方形ABEF不共面,N、M分别在AE和BD上,AN=DM.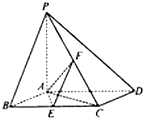 如图,已知四棱锥P-ABCD,底面ABCD是边长为2的菱形,PA⊥平面ABCD,∠ABC=60°,E、F分别是BC、PC的中点.
如图,已知四棱锥P-ABCD,底面ABCD是边长为2的菱形,PA⊥平面ABCD,∠ABC=60°,E、F分别是BC、PC的中点.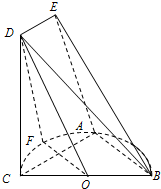 如图:已知BC是半径为1的半圆O的直径,A是半圆周上不同于B,C的点,F为弧AC的中点.在梯形ACDE中,DE∥AC且AC=2DE,平面ACDE⊥平面ABC.求证:
如图:已知BC是半径为1的半圆O的直径,A是半圆周上不同于B,C的点,F为弧AC的中点.在梯形ACDE中,DE∥AC且AC=2DE,平面ACDE⊥平面ABC.求证: