题目内容
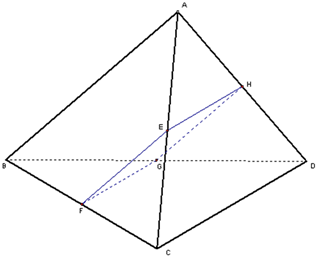
 已知:正方形ABCD与正方形ABEF不共面,N、M分别在AE和BD上,AN=DM.
已知:正方形ABCD与正方形ABEF不共面,N、M分别在AE和BD上,AN=DM.求证:MN∥平面BCE.
考点:直线与平面平行的判定
专题:证明题,空间位置关系与距离
分析:(方法一)利用线面平行的判定定理,进行证明;
(方法二)利用线面平行的判定定理,进行证明.
(方法二)利用线面平行的判定定理,进行证明.
解答:
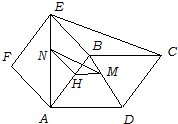 证明:(方法一)
证明:(方法一)
连结AM并延长交BC于G
则
=
=
所以MN∥EG…5’
又MN?平面BCE
EG?平面BCE
故MN∥平面BCE…10’
(方法二)过N做直线NH∥EB交直线AB于H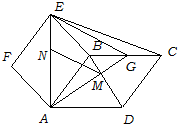
连结MH
因为
=
=
所以HM∥AD∥BC…5’
于是平面MHN∥平面CBE
MN?平面MHN
所以MN∥平面BCE…10’
 证明:(方法一)
证明:(方法一)连结AM并延长交BC于G
则
| AN |
| NE |
| DM |
| MB |
| AM |
| MG |
所以MN∥EG…5’
又MN?平面BCE
EG?平面BCE
故MN∥平面BCE…10’
(方法二)过N做直线NH∥EB交直线AB于H

连结MH
因为
| BH |
| HA |
| EN |
| NA |
| BM |
| MD |
所以HM∥AD∥BC…5’
于是平面MHN∥平面CBE
MN?平面MHN
所以MN∥平面BCE…10’
点评:本题是中档题,考查直线与平面的平行的证明方法,注意定理条件的正确应用,考查空间想象能力.

练习册系列答案
相关题目
已知
=-
,则
的值是( )
| 1+sinα |
| cosα |
| 1 |
| 2 |
| cosα |
| 1-sinα |
A、
| ||
B、-
| ||
| C、2 | ||
| D、-2 |