题目内容
函数函数f（x）=x2-4x+5-2lnx的零点个数为（ ）
| A、3 | B、2 | C、1 | D、0 |
考点：函数零点的判定定理
专题：函数的性质及应用
分析：将函数的零点问题转化为方程的根的问题，进一步转化为函数图象的交点问题．
解答：
解：由题意可得x＞0，求函数f（x）=x2-4x+5-2lnx的零点个数，
即求方程lnx=
（x-2）2+
的解的个数．
数形结合可得，
函数y=lnx的图象（蓝线部分）和函数y=
（x-2）2+
（红线部分）的图象有2个交点，
故f（x）=lnx-x2+2x+5有两个零点，
故选：B．
解：由题意可得x＞0，求函数f（x）=x2-4x+5-2lnx的零点个数，即求方程lnx=
| 1 |
| 2 |
| 1 |
| 2 |
数形结合可得，
函数y=lnx的图象（蓝线部分）和函数y=
| 1 |
| 2 |
| 1 |
| 2 |
故f（x）=lnx-x2+2x+5有两个零点，
故选：B．
点评：本题考查了函数零点的定义，即对应方程f（x）=0的根，是基础题．
练习册系列答案
阅读快车系列答案
相关题目
已知x，y∈R+，且xy2=8，则4x+y的最小值为（ ）
A、4
| ||
B、6
| ||
| C、6 | ||
| D、2 |
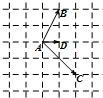已知向量| AC |
| AD |
| AB |
| AC |
| AB |
| AD |
| A、2 | B、-2 | C、3 | D、-3 |
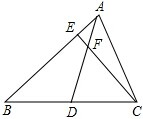如图，已知△ABC中，AE：EB=1：3，BD：DC=2：1，AD与CE相交于点F，则| EF |
| FC |
| AF |
| FD |
A、
| ||
| B、1 | ||
C、
| ||
| D、2 |
己知函数f（x）=Acos（ωx+φ）（A＞0，ω＞0，0＜φ＜π）为奇函数，该函数的部分图象如图所示，△EFG是边长为2的等边三角形，则f（-1）的值为（ ）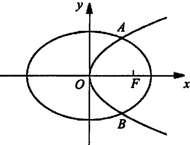
如图，已知椭圆C1：
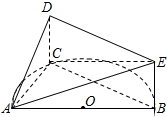如图，AB是半圆O的直径，C是半圆O上除A、B外的一个动点，DC⊥平面ABC，DC∥BE，CD=BE，AB=4，tan∠EAB=