题目内容
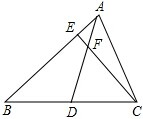如图，已知△ABC中，AE：EB=1：3，BD：DC=2：1，AD与CE相交于点F，则| EF |
| FC |
| AF |
| FD |
A、
| ||
| B、1 | ||
C、
| ||
| D、2 |
考点：与圆有关的比例线段
专题：立体几何
分析：先过E作EG∥BC，交AD于G，再作DH∥BC交CE于H，由平行线分线段成比例定理的推论，再结合已知条件，可分别求出
和
的值，相加即可．
| EF |
| EC |
| AF |
| AD |
解答：
解：作EG∥BC交AD于G，则有
=
，即
=
，得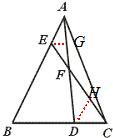
EG=
BD=
CD，
∴
=
=
，
作DH∥AB交CE于H，则DH=
BE=AE，
∴
=
=1，
∴
+
=
+1=
．
故选：C．
| AE |
| EB |
| 1 |
| 3 |
| AE |
| AB |
| 1 |
| 4 |
EG=
| 1 |
| 4 |
| 1 |
| 2 |
∴
| EF |
| FC |
| EG |
| CD |
| 1 |
| 2 |
作DH∥AB交CE于H，则DH=
| 1 |
| 3 |
∴
| AF |
| FD |
| AE |
| DH |
∴
| EF |
| FC |
| AF |
| FD |
| 1 |
| 2 |
| 3 |
| 2 |
故选：C．
点评：本题考查了相似三角形的性质：相似三角形的对应角相等，对应边的比相等，解题时要注意比例式的变形．
练习册系列答案
名校课堂系列答案
相关题目
已知向量
=（-1，1），
=（2，x），若
⊥（
+
），则实数x的值为（ ）
| a |
| b |
| a |
| a |
| b |
| A、0 | B、1 | C、2 | D、4 |
已知x，y∈R，且命题p：x＞y，命题q：x-y+sin（x-y）＞0，则p是q的（ ）
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |
y=x3在点M（-2，-8）处的切线方程是（ ）
| A、12x-y-16=0 |
| B、12x-y+16=0 |
| C、12x+y-16=0 |
| D、12x+y+16=0 |
y=cosx•sinx是（ ）
| A、奇函数 |
| B、偶函数 |
| C、既是奇函数也是偶函数 |
| D、既不是奇函数也不是偶函数 |
已知命题“若p，则q”是真命题，对下列命题中一定是真命题的是（ ）
| A、若q，则p |
| B、￢p，则￢q |
| C、若￢q，则￢p |
| D、若￢p，则q |
函数函数f（x）=x2-4x+5-2lnx的零点个数为（ ）
| A、3 | B、2 | C、1 | D、0 |
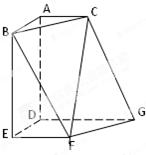如图，在多面体ABCDEFG中，平面ABC∥平面DEFG，AD⊥平面DEFG，BA⊥AC，ED⊥DG，EF∥DG且AC=1，AB=ED=EF=2，AD=DG=4．