题目内容
9.若先将函数$y=\sqrt{3}sin({x-\frac{π}{6}})+cos({x-\frac{π}{6}})$图象上各点的纵坐标不变,横坐标伸长到原来的2倍,再将所得图象向左平移$\frac{π}{6}$个单位,所得函数图象的一条对称轴的方程是( )| A. | $x=\frac{π}{6}$ | B. | $x=\frac{π}{3}$ | C. | $x=\frac{π}{2}$ | D. | $x=\frac{5π}{6}$ |
分析 利用两角和的正弦函数公式化简已知可得y=2sinx,利用函数y=Asin(ωx+φ)的图象变换规律及正弦函数的图象和性质即可得解.
解答 解:∵$y=\sqrt{3}sin({x-\frac{π}{6}})+cos({x-\frac{π}{6}})$=2sin[(x-$\frac{π}{6}$)+$\frac{π}{6}$]=2sinx,
∴先将函数图象上各点的纵坐标不变,横坐标伸长到原来的2倍,可得函数为:y=2sin$\frac{1}{2}$x,
再将所得图象向左平移$\frac{π}{6}$个单位,所得函数为:y=2sin$\frac{1}{2}$(x+$\frac{π}{6}$)=2sin($\frac{x}{2}$+$\frac{π}{12}$),
∴由$\frac{x}{2}$+$\frac{π}{12}$=kπ+$\frac{π}{2}$,k∈Z,可解得对称轴的方程是:x=2kπ+$\frac{5π}{6}$,k∈Z,当k=0时,可得函数图象的一条对称轴的方程是:x=$\frac{5π}{6}$.
故选:D.
点评 本题主要考查了两角和的正弦函数公式,函数y=Asin(ωx+φ)的图象变换规律及正弦函数的图象和性质,属于基本知识的考查.

练习册系列答案
相关题目
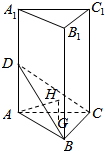 如图所示,三棱柱ABC-A1B1C1的底面是正三角形,侧棱AA1⊥底面ABC,AB=1,AA1=2,点D在侧棱AA1上,点G,H分别是△ABC,△BCD的重心.
如图所示,三棱柱ABC-A1B1C1的底面是正三角形,侧棱AA1⊥底面ABC,AB=1,AA1=2,点D在侧棱AA1上,点G,H分别是△ABC,△BCD的重心.