题目内容
19.已知实数x、y满足方程y2=x,求函数z=$\frac{y-1}{x+2}$最值.分析 作出抛物线y2=x的图形,由函数z=$\frac{y-1}{x+2}$的几何意义是抛物线上的点(x,y)与定点(-2,1)的斜率.设出切线的方程,联立抛物线的方程,运用判别式为0,解方程即可得到所求的最值.
解答 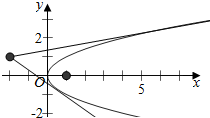 解:作出抛物线y2=x的图形,
解:作出抛物线y2=x的图形,
函数z=$\frac{y-1}{x+2}$的几何意义是抛物线上的点(x,y)
与定点(-2,1)的斜率.
过点(-2,1)作抛物线的切线,
设方程为y-1=k(x+2),即y=kx+2k+1,
代入抛物线的方程,
可得k2x2+(4k2+2k-1)x+(2k+1)2=0,
由相切的条件可得,△=(4k2+2k-1)2-4k2(2k+1)2=0,
解方程可得k=$\frac{-1±\sqrt{3}}{4}$.
则函数z的最小值为$\frac{-1-\sqrt{3}}{4}$,最大值为$\frac{-1+\sqrt{3}}{4}$.
点评 本题考查函数的最值的求法,注意运用几何意义:直线的斜率,同时考查直线和抛物线相切的条件,考查运算能力,属于中档题.

练习册系列答案
 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案
相关题目
9.若先将函数$y=\sqrt{3}sin({x-\frac{π}{6}})+cos({x-\frac{π}{6}})$图象上各点的纵坐标不变,横坐标伸长到原来的2倍,再将所得图象向左平移$\frac{π}{6}$个单位,所得函数图象的一条对称轴的方程是( )
| A. | $x=\frac{π}{6}$ | B. | $x=\frac{π}{3}$ | C. | $x=\frac{π}{2}$ | D. | $x=\frac{5π}{6}$ |
10.一个4×4×h的长方体能装下8个半径为1的小球和一个半径为2的大球,则h的最小值为( )
| A. | 2$\sqrt{6}$+2 | B. | 2$\sqrt{7}$+2 | C. | 4$\sqrt{2}$+2 | D. | 8 |
8.若抛物线y2=2px(p≠0)的准线与圆x2+y2+2x-3=0相切,则p的值为( )
| A. | 2 | B. | ±2 | C. | ±6 | D. | 6或-2 |