题目内容
20.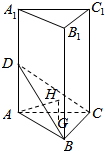 如图所示,三棱柱ABC-A1B1C1的底面是正三角形,侧棱AA1⊥底面ABC,AB=1,AA1=2,点D在侧棱AA1上,点G,H分别是△ABC,△BCD的重心.
如图所示,三棱柱ABC-A1B1C1的底面是正三角形,侧棱AA1⊥底面ABC,AB=1,AA1=2,点D在侧棱AA1上,点G,H分别是△ABC,△BCD的重心.(1)求证:GH∥AD;
(2)当AH=$\frac{\sqrt{3}}{2}$时,求AD的长.
分析 (1)取BC的中点E,连接AE,DE,根据重心的定义和性质,可得GH:HE=AG:GE=2:1,再由平行线分线段成比例定理的逆定理得到结论;
(2)根据AB=1,依次计算AE,AG,GH,AD的长度,可得答案.
解答 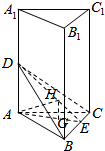 证明:(1)取BC的中点E,连接AE,DE,
证明:(1)取BC的中点E,连接AE,DE,
∵点G,H分别是△ABC,△BCD的重心.
∴G在AE上,H在DE上,
且GH:HE=AG:GE=2:1,
∴GH∥AD;
(2)∵AB=1,
∴AE=$\sqrt{{1}^{2}-(\frac{1}{2})^{2}}$=$\frac{\sqrt{3}}{2}$,
∴AG=$\frac{2}{3}$AE=$\frac{2}{3}•\frac{\sqrt{3}}{2}$=33,
又∵AH=$\frac{\sqrt{3}}{2}$,
∴GH=$\sqrt{{AH}^{2}-{AG}^{2}}$=$\sqrt{(\frac{\sqrt{3}}{2})^{2}-(\frac{\sqrt{3}}{3})^{2}}$=$\frac{\sqrt{15}}{6}$,
∴AD=3GH=$\frac{\sqrt{15}}{2}$
点评 本题考查的知识点是三角形的五心,平行线分线段成比例定理的逆定理,勾股定理,难度中档.

练习册系列答案
 导学全程练创优训练系列答案
导学全程练创优训练系列答案
相关题目
8.函数f(x)=3-2sin2x是( )
| A. | 最小正周期为2π的偶函数 | B. | 最小正周期为2π的奇函数 | ||
| C. | 最小正周期为π的偶函数 | D. | 最小正周期为π的奇函数 |
12.设函数$f(x)=\left\{{\begin{array}{l}{\sqrt{x-1}}&{x≥1}\\ 1&{x<1}\end{array}}\right.$,则$f({f({f({\frac{π}{2}})})})$的值为( )
| A. | 0 | B. | 1 | C. | $\sqrt{\frac{π}{2}-1}$ | D. | $\sqrt{\sqrt{\frac{π}{2}-1}-1}$ |
9.若先将函数$y=\sqrt{3}sin({x-\frac{π}{6}})+cos({x-\frac{π}{6}})$图象上各点的纵坐标不变,横坐标伸长到原来的2倍,再将所得图象向左平移$\frac{π}{6}$个单位,所得函数图象的一条对称轴的方程是( )
| A. | $x=\frac{π}{6}$ | B. | $x=\frac{π}{3}$ | C. | $x=\frac{π}{2}$ | D. | $x=\frac{5π}{6}$ |
10.一个4×4×h的长方体能装下8个半径为1的小球和一个半径为2的大球,则h的最小值为( )
| A. | 2$\sqrt{6}$+2 | B. | 2$\sqrt{7}$+2 | C. | 4$\sqrt{2}$+2 | D. | 8 |