题目内容
若0<α<
,-
<β<0,且sinβ=-
,cos(α-β)=
,则sinα= .
| π |
| 2 |
| π |
| 2 |
| 5 |
| 13 |
| 3 |
| 5 |
考点:两角和与差的正弦函数
专题:计算题,三角函数的求值
分析:利用同角三角函数平方关系,求出cosβ、sin(α-β),再利用角的变换,即可得出结论.
解答:
解:∵sinβ=-
,-
<β<0,
∴cosβ=
,
∵0<α<
,-
<β<0,
∴0<α-β<π,
∵cos(α-β)=
,
∴sin(α-β)=
,
∴sinα=sin[(α-β)+β]=sin(α-β)cosβ+cos(α-β)sinβ=
•
+
•(-
)=
.
故答案为:
.
| 5 |
| 13 |
| π |
| 2 |
∴cosβ=
| 12 |
| 13 |
∵0<α<
| π |
| 2 |
| π |
| 2 |
∴0<α-β<π,
∵cos(α-β)=
| 3 |
| 5 |
∴sin(α-β)=
| 4 |
| 5 |
∴sinα=sin[(α-β)+β]=sin(α-β)cosβ+cos(α-β)sinβ=
| 4 |
| 5 |
| 12 |
| 13 |
| 3 |
| 5 |
| 5 |
| 13 |
| 33 |
| 65 |
故答案为:
| 33 |
| 65 |
点评:本题考查两角和与差的正弦函数,考查同角三角函数平方关系、角的变换,正确运用sinα=sin[(α-β)+β]=sin(α-β)cosβ+cos(α-β)sinβ是关键.

练习册系列答案
 导学全程练创优训练系列答案
导学全程练创优训练系列答案
相关题目
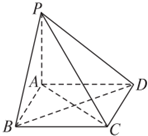 已知PA垂直于正方形ABCD所在平面,连接PB、PC、PD、AC、BD,则下列垂直关系中正确的序号是
已知PA垂直于正方形ABCD所在平面,连接PB、PC、PD、AC、BD,则下列垂直关系中正确的序号是