题目内容
18．已知i是虚数单位，a∈R，复数z1=3-ai，z2=1+2i，若z1•z2是纯虚数，则a=（ ）| A． | -$\frac{3}{2}$ | B． | $\frac{3}{2}$ | C． | -6 | D． | 6 |
分析 利用复数的运算法则、纯虚数的定义即可得出．
解答 解：复数z1=3-ai，z2=1+2i，
∴z1•z2=（3-ai）（1+2i）=3+2a+（6-a）i是纯虚数，
∴$\left\{\begin{array}{l}{3+2a=0}\\{6-a≠0}\end{array}\right.$，解得a=-$\frac{3}{2}$．
故选：A．
点评 本题考查了复数的运算法则、纯虚数的定义，考查了推理能力与计算能力，属于基础题．
练习册系列答案
优加精卷系列答案
相关题目
8．在正方体ABCD-A1B1C1D1中，P是A1D上的一点，且满足A1P=2PD，下列命题正确的是（ ）
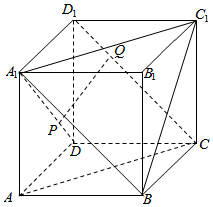
| A． | 在CD1上存在点Q，使得PQ∥平面AA1C1C | |
| B． | 在CD1上存在点Q，使得PQ⊥平面AA1C1C | |
| C． | 在CD1上存在点Q，使得PQ∥平面A1BC1 | |
| D． | 在CD1上存在点Q，使得PQ⊥平面A1BC1 |
6．若x，y满足$\left\{\begin{array}{l}x-y≥0\\ x+y≤1\\ y≥0.\end{array}\right.$，则z=x+2y的最大值为（ ）
| A． | 0 | B． | 1 | C． | 2 | D． | $\frac{3}{2}$ |
10．对于数列{an}，“an+1＜|an|（n=1，2，…）”是“{an}为递减数列”的（ ）
| A． | 充分不必要条件 | B． | 必要不充分条件 | ||
| C． | 必要条件 | D． | 既不充分也不必要条件 |