题目内容
7.已知向量$\overrightarrow{a}$=(x,1)在$\overrightarrow{b}$=(1,$\sqrt{3}$)方向上的投影为$\sqrt{3}$,则x=$\sqrt{3}$.分析 根据平面向量数量积的坐标计算以及几何意义,得到所求.
解答 解:由已知得到$\overrightarrow{a}•\overrightarrow{b}$=x+$\sqrt{3}$,向量$\overrightarrow{a}$=(x,1)在$\overrightarrow{b}$=(1,$\sqrt{3}$)方向上的投影为$\sqrt{3}$,
设α为两个向量的夹角,则$|\overrightarrow{a}|cosα=\frac{\overrightarrow{a}•\overrightarrow{b}}{|\overrightarrow{b}|}=\sqrt{3}$,所以$\sqrt{3}=\frac{x+\sqrt{3}}{2}$,解得x=$\sqrt{3}$;
故答案为:$\sqrt{3}$.
点评 本题考查了平面向量的数量积公式的运用以及投影;关键是明确数量积与投影的关系;属于基础题.

练习册系列答案
相关题目
18.已知i是虚数单位,a∈R,复数z1=3-ai,z2=1+2i,若z1•z2是纯虚数,则a=( )
| A. | -$\frac{3}{2}$ | B. | $\frac{3}{2}$ | C. | -6 | D. | 6 |
15.已知集合M={x|x2+x-12≤0},N={y|y=3x,x≤1},则集合{x|x∈M且x∉N}为( )
| A. | (0,3] | B. | [-4,3] | C. | [-4,0) | D. | [-4,0] |
19.已知O为坐标原点,F为抛物线y2=4x的焦点,直线l:y=m(x-1)与抛物线交于A,B两点,点A在第一象限,若|FA|=3|FB|.则m的值为( )
| A. | 3 | B. | $\sqrt{3}$ | C. | $\frac{\sqrt{3}}{3}$ | D. | $\frac{1}{3}$ |
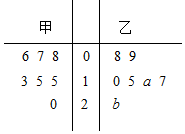 甲、乙两家快餐店对某日7个时段光顺的客人人数进行统计并绘制茎叶图如图所示(下面简称甲数据、乙数据),且乙数据的众数为17,甲数据的平均数比乙数据平均数少2.
甲、乙两家快餐店对某日7个时段光顺的客人人数进行统计并绘制茎叶图如图所示(下面简称甲数据、乙数据),且乙数据的众数为17,甲数据的平均数比乙数据平均数少2.