题目内容
6.若x,y满足$\left\{\begin{array}{l}x-y≥0\\ x+y≤1\\ y≥0.\end{array}\right.$,则z=x+2y的最大值为( )| A. | 0 | B. | 1 | C. | 2 | D. | $\frac{3}{2}$ |
分析 作出不等式对应的平面区域,利用线性规划的知识,通过平移即可求z的最大值.
解答 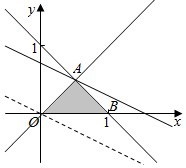 解:作出不等式对应的平面区域,
解:作出不等式对应的平面区域,
由z=x+2y,得y=-$\frac{1}{2}x+\frac{z}{2}$,
平移直线y=-$\frac{1}{2}x+\frac{z}{2}$,由图象可知当直线y=-$\frac{1}{2}x+\frac{z}{2}$经过点A时,直线y=-$\frac{1}{2}x+\frac{z}{2}$的截距最大,此时z最大.
由$\left\{\begin{array}{l}{x-y=0}\\{x+y=1}\end{array}\right.$,得$\left\{\begin{array}{l}{x=\frac{1}{2}}\\{y=\frac{1}{2}}\end{array}\right.$,
即A($\frac{1}{2}$,$\frac{1}{2}$),
此时z的最大值为z=$\frac{1}{2}$+2×$\frac{1}{2}$=$\frac{3}{2}$,
故选:D.
点评 本题主要考查线性规划的应用,利用图象平行求得目标函数的最大值,利用数形结合是解决线性规划问题中的基本方法.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
1.记样本x1,x2,…,xm的平均数为$\overline{x}$,样本y1,y2,…,yn的平均数为$\overline{y}$($\overline{x}$≠$\overline{y}$),若样本x1,x2,…,xm,y1,y2,…,yn的平均数为$\overline{z}$=$\frac{1}{4}$$\overline{x}$+$\frac{3}{4}$$\overline{y}$,则$\frac{m}{n}$的值为( )
| A. | 3 | B. | 4 | C. | $\frac{1}{4}$ | D. | $\frac{1}{3}$ |
11.下列函数中,既是奇函数又在区间(0,+∞)上单调递增的是( )
| A. | y=x3 | B. | y=lnx | C. | y=sinx | D. | y=2x |
18.已知i是虚数单位,a∈R,复数z1=3-ai,z2=1+2i,若z1•z2是纯虚数,则a=( )
| A. | -$\frac{3}{2}$ | B. | $\frac{3}{2}$ | C. | -6 | D. | 6 |
15.已知集合M={x|x2+x-12≤0},N={y|y=3x,x≤1},则集合{x|x∈M且x∉N}为( )
| A. | (0,3] | B. | [-4,3] | C. | [-4,0) | D. | [-4,0] |
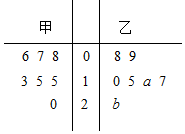 甲、乙两家快餐店对某日7个时段光顺的客人人数进行统计并绘制茎叶图如图所示(下面简称甲数据、乙数据),且乙数据的众数为17,甲数据的平均数比乙数据平均数少2.
甲、乙两家快餐店对某日7个时段光顺的客人人数进行统计并绘制茎叶图如图所示(下面简称甲数据、乙数据),且乙数据的众数为17,甲数据的平均数比乙数据平均数少2.