题目内容
已知函数f(x)=lg(
)为奇函数.
(1)求m的值,并求f(x)的定义域;
(2)判断函数f(x)的单调性,并证明;
(3)若对于任意θ∈[0,
],是否存在实数λ,使得不等式f(cos2θ+λsinθ-
)-lg3>0.若存在,求出实数λ的取值范围;若不存在,请说明理由.
| 1-mx |
| 1-x |
(1)求m的值,并求f(x)的定义域;
(2)判断函数f(x)的单调性,并证明;
(3)若对于任意θ∈[0,
| π |
| 2 |
| 1 |
| 3 |
考点:对数函数图象与性质的综合应用
专题:函数的性质及应用
分析:(1)根据函数奇偶性的条件建立方程关系,即可求m的值,
(2)根据函数单调性的定义即可判断函数f(x)的单调性;
(3)利用三角函数姜不等式进行转化,解三角不等式即可得到结论.
(2)根据函数单调性的定义即可判断函数f(x)的单调性;
(3)利用三角函数姜不等式进行转化,解三角不等式即可得到结论.
解答:
解:(1)∵函数f(x)=lg(
)为奇函数,
∴f(-x)=-f(x)在定义域内恒成立,
即lg(
)=-lg(
),
即lg(
)+lg(
)=0,
则
•
=1,即1-m2x2=1-x2,在定义域内恒成立,
∴m=-1或m=1,当m=1时,f(x)=lg(
)=lg1=0,
∴m=-1,此时f(x)=lg
,
由
>0,解得-1<x<1,
故函数的定义域是(-1,1).
(2)∵f(x)=lg
,-1<x<1,任取-1<x1<x2<1,
设u(x)=
,-1<x<1,
则u(x1)-u(x2)=
-
=
∵-1<x1<x2<1,∴u(x1)-u(x2)<0,∴u(x1)<u(x2),即lgu(x1)<lgu(x2),
∴f(x1)<f(x2),即f(x)在定义域内单调递增.
(3)假设存在实数λ,使得不等式不等式f(cos2θ+λsinθ-
)-lg3>0成立,
即不等式f(cos2θ+λsinθ-
)>lg3=f(
),
由(1),(2)知:
<cos2θ+λsinθ-
<1 对于任意θ∈[0,
],
即
,当θ=0时成立;
当θ∈(0,
]时,令sinθ=t,则
,
即
,则
<λ<
.
| 1-mx |
| 1-x |
∴f(-x)=-f(x)在定义域内恒成立,
即lg(
| 1+mx |
| 1+x |
| 1-mx |
| 1-x |
即lg(
| 1+mx |
| 1+x |
| 1-mx |
| 1-x |
则
| 1+mx |
| 1+x |
| 1-mx |
| 1-x |
∴m=-1或m=1,当m=1时,f(x)=lg(
| 1-mx |
| 1-x |
∴m=-1,此时f(x)=lg
| 1+x |
| 1-x |
由
| 1+x |
| 1-x |
故函数的定义域是(-1,1).
(2)∵f(x)=lg
| 1+x |
| 1-x |
设u(x)=
| 1+x |
| 1-x |
则u(x1)-u(x2)=
| 1+x1 |
| 1-x1 |
| 1+x2 |
| 1-x2 |
| 2(x1-x2) |
| (1-x1)(1-x2) |
∵-1<x1<x2<1,∴u(x1)-u(x2)<0,∴u(x1)<u(x2),即lgu(x1)<lgu(x2),
∴f(x1)<f(x2),即f(x)在定义域内单调递增.
(3)假设存在实数λ,使得不等式不等式f(cos2θ+λsinθ-
| 1 |
| 3 |
即不等式f(cos2θ+λsinθ-
| 1 |
| 3 |
| 1 |
| 2 |
由(1),(2)知:
| 1 |
| 2 |
| 1 |
| 3 |
| π |
| 2 |
即
|
当θ∈(0,
| π |
| 2 |
|
即
|
| 5 |
| 6 |
2
| ||
| 3 |
点评:本题主要考查函数性质的综合应用,要求熟练掌握函数奇偶性和单调性的判断和应用.

练习册系列答案
相关题目
 如图所示,在正方体ABCD-A1B1C1D1中,E、F、G、H分别是BC、C1C、C1D1、A1A的中点.求证:
如图所示,在正方体ABCD-A1B1C1D1中,E、F、G、H分别是BC、C1C、C1D1、A1A的中点.求证: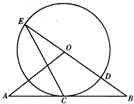 如图,直线AB经过⊙O上一点C,且OA=OB,CA=CB,⊙O交直线OB于点E、D.
如图,直线AB经过⊙O上一点C,且OA=OB,CA=CB,⊙O交直线OB于点E、D.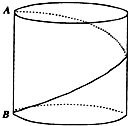 如图,底面半径为1,高为2的圆柱,有A点有一只蚂蚁,现在这只蚂蚁要围绕圆柱由A点爬到B点,问蚂蚁爬行的最短距离是多少?
如图,底面半径为1,高为2的圆柱,有A点有一只蚂蚁,现在这只蚂蚁要围绕圆柱由A点爬到B点,问蚂蚁爬行的最短距离是多少?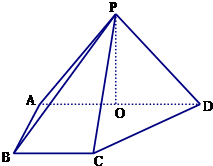 如图,在四棱锥P-ABCD中,侧面PAD⊥底面ABCD,侧棱PA=PD=
如图,在四棱锥P-ABCD中,侧面PAD⊥底面ABCD,侧棱PA=PD= 如图,BC为圆O的直径,D为圆周上异于B、C的一点,AB垂直于圆O所在的平面,BE⊥AC于点E,BF⊥AD于点F.
如图,BC为圆O的直径,D为圆周上异于B、C的一点,AB垂直于圆O所在的平面,BE⊥AC于点E,BF⊥AD于点F. 如图所示,等腰△ABC的底边AB=6
如图所示,等腰△ABC的底边AB=6