题目内容
 如图所示,等腰△ABC的底边AB=6
如图所示,等腰△ABC的底边AB=6| 6 |
(Ⅰ)求S(x)和V(x)的表达式;
(Ⅱ)当x为何值时,V(x)取得最大值?
(Ⅲ)说明异面直线AP与EF所成的角θ与x的变化是否有关系,若无关,写出θ的值(不必写出理由与过程).
考点:点、线、面间的距离计算,导数在最大值、最小值问题中的应用
专题:空间位置关系与距离,空间角
分析:( I)由折起的过程知,PE⊥平面ABC,由此能求出S(x)和V(x)的表达式.
( II)V′(x)=
(9-
x2),利用导数性质得x=6时,V(x)取得最大值12
.
(Ⅲ)异面直线AP与EF所成的角θ与x的变化无关,θ=
.
( II)V′(x)=
| ||
| 3 |
| 1 |
| 4 |
| 6 |
(Ⅲ)异面直线AP与EF所成的角θ与x的变化无关,θ=
| π |
| 2 |
解答:
解:( I)由折起的过程知,
PE⊥平面ABC,
S△ABC=9
,
S△BEF=
•S△BDC=
x2
V(x)=
x(9-
x2)(0<x<3
).…(5分)
( II)V′(x)=
(9-
x2),
所以x∈(0,6)时,v'(x)>0,V(x)单调递增;
6<x<3
时v'(x)<0,V(x)单调递减;
因此x=6时,V(x)取得最大值12
;…(10分)
(Ⅲ)异面直线AP与EF所成的角θ与x的变化无关,θ=
.…(14分)
PE⊥平面ABC,
S△ABC=9
| 6 |
S△BEF=
| x2 |
| 54 |
| ||
| 12 |
V(x)=
| ||
| 3 |
| 1 |
| 12 |
| 6 |
( II)V′(x)=
| ||
| 3 |
| 1 |
| 4 |
所以x∈(0,6)时,v'(x)>0,V(x)单调递增;
6<x<3
| 6 |
因此x=6时,V(x)取得最大值12
| 6 |
(Ⅲ)异面直线AP与EF所成的角θ与x的变化无关,θ=
| π |
| 2 |
点评:本题考查三角形面积和四棱锥体积的求法,考查体积的最大值的求法,考查异面直线所成的角的求法,解题时要认真审题,注意空间思维能力的培养.

练习册系列答案
相关题目
 如图,在四棱柱ABCD-A1B1C1D1中,侧棱AA1⊥底面ABCD,AB∥DC,AA1=1,AB=3k,AD=4k,BC=5k,DC=6k(k>0).
如图,在四棱柱ABCD-A1B1C1D1中,侧棱AA1⊥底面ABCD,AB∥DC,AA1=1,AB=3k,AD=4k,BC=5k,DC=6k(k>0).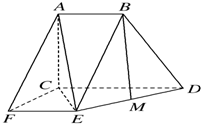 在直角梯形CDEF中,DC⊥CF,DC∥EF,CD=CF=2EF=2.将它绕CD旋转得到CDBA,使得平面CDBA⊥平面CDEF.
在直角梯形CDEF中,DC⊥CF,DC∥EF,CD=CF=2EF=2.将它绕CD旋转得到CDBA,使得平面CDBA⊥平面CDEF. 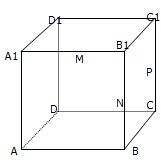 如图,在棱长为1的正方形ABCD-A1B1C1D1中,M、N、P分别为A1B1、BB1、CC1的中点.
如图,在棱长为1的正方形ABCD-A1B1C1D1中,M、N、P分别为A1B1、BB1、CC1的中点.