题目内容
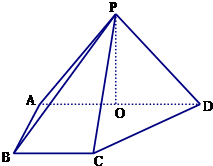 如图,在四棱锥P-ABCD中,侧面PAD⊥底面ABCD,侧棱PA=PD=
如图,在四棱锥P-ABCD中,侧面PAD⊥底面ABCD,侧棱PA=PD=| 2 |
(1)求直线PB与平面POC所成角的余弦值.
(2)求B点到平面PCD的距离.
(3)线段PD上是否存在一点Q,使得二面角Q-AC-D的余弦值为
| ||
| 3 |
| PQ |
| QD |
考点:点、线、面间的距离计算,直线与平面所成的角
专题:综合题,空间位置关系与距离,空间角
分析:(1)先证明直线PO垂直平面ABCD中的两条相交直线垂直,可得PO⊥平面ABCD,建立空间直角坐标系,确定平面POC的法向量,利用向量的夹角公式,即可求直线PB与平面POC所成角的余弦值.
(2)求出平面PDC的法向量,利用距离公式,可求B点到平面PCD的距离.
(3)假设存在,则设
=λ
(0<λ<1),求出平面CAQ的法向量、平面CAD的法向量
=(0,0,1),根据二面角Q-AC-D的余弦值为
,利用向量是夹角公式,即可求得结论.
(2)求出平面PDC的法向量,利用距离公式,可求B点到平面PCD的距离.
(3)假设存在,则设
| PQ |
| PD |
| n |
| ||
| 3 |
解答:
 解:(1)在△PAD中PA=PD,O为AD中点,所以PO⊥AD,
解:(1)在△PAD中PA=PD,O为AD中点,所以PO⊥AD,
又侧面PAD⊥底面ABCD,平面PAD∩平面ABCD=AD,PO?平面PAD,
所以PO⊥平面ABCD.
又在直角梯形ABCD中,易得OC⊥AD;
所以以O为原点,OC为x轴,OD为y轴,OP为z轴建立空间直角坐标系.
则P(0,0,1),A(0,-1,0),B(1,-1,0),C(1,0,0),D(0,1,0);
所以
=(1,-1,-1),易证:OA⊥平面POC,
所以
=(0,-1,0),平面POC的法向量,
COS<
,
>=
=
所以PB与平面POC所成角的余弦值为
….(4分)
(2)
=(1,-1,-1),设平面PDC的法向量为
=(x,y,z),
则
,取z=1得
=(1,1,1)
B点到平面PCD的距离d=
=
….(8分)
(3)假设存在,则设
=λ
(0<λ<1)
因为
=(0,1,-1),所以Q(0,λ,1-λ).
设平面CAQ的法向量为
=(a,b,c),则
,
所以取
=(1-λ,λ-1,λ+1),
平面CAD的法向量
=(0,0,1),
因为二面角Q-AC-D的余弦值为
,
所以
=
,
所以3λ2-10λ+3=0.
所以λ=
或λ=3(舍去),
所以
=
-------------(12分)
 解:(1)在△PAD中PA=PD,O为AD中点,所以PO⊥AD,
解:(1)在△PAD中PA=PD,O为AD中点,所以PO⊥AD,又侧面PAD⊥底面ABCD,平面PAD∩平面ABCD=AD,PO?平面PAD,
所以PO⊥平面ABCD.
又在直角梯形ABCD中,易得OC⊥AD;
所以以O为原点,OC为x轴,OD为y轴,OP为z轴建立空间直角坐标系.
则P(0,0,1),A(0,-1,0),B(1,-1,0),C(1,0,0),D(0,1,0);
所以
| PB |
所以
| OA |
COS<
| PB |
| OA |
| ||||
|
|
| ||
| 3 |
所以PB与平面POC所成角的余弦值为
| ||
| 3 |
(2)
| PB |
| u |
则
|
| u |
B点到平面PCD的距离d=
|
| ||||
|
|
| ||
| 3 |
(3)假设存在,则设
| PQ |
| PD |
因为
| PD |
设平面CAQ的法向量为
| m |
|
所以取
| m |
平面CAD的法向量
| n |
因为二面角Q-AC-D的余弦值为
| ||
| 3 |
所以
|
| ||||
|
|
| ||
| 3 |
所以3λ2-10λ+3=0.
所以λ=
| 1 |
| 3 |
所以
| PQ |
| QD |
| 1 |
| 2 |
点评:本题主要考查直线与平面的位置关系、直线与平面所成角、点到平面的距离等基本知识,考查空间想象能力,逻辑思维能力和运算能力.

练习册系列答案
 同步轻松练习系列答案
同步轻松练习系列答案 课课通课程标准思维方法与能力训练系列答案
课课通课程标准思维方法与能力训练系列答案
相关题目
已知a=(
)x,b=(
)x-1,c=log
x,且x>1,则( )
| 2 |
| 3 |
| 3 |
| 2 |
| 2 |
| 3 |
| A、a>b>c |
| B、b>a>c |
| C、c>a>b |
| D、b>c>a |
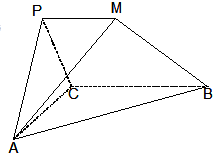 在如图所示的多面体PMBCA中,平面PAC⊥平面ABC,△PAC是边长为2的正三角形,PM∥BC,且BC=2PM=4,AB=2
在如图所示的多面体PMBCA中,平面PAC⊥平面ABC,△PAC是边长为2的正三角形,PM∥BC,且BC=2PM=4,AB=2 如图,在四棱柱ABCD-A1B1C1D1中,侧棱AA1⊥底面ABCD,AB∥DC,AA1=1,AB=3k,AD=4k,BC=5k,DC=6k(k>0).
如图,在四棱柱ABCD-A1B1C1D1中,侧棱AA1⊥底面ABCD,AB∥DC,AA1=1,AB=3k,AD=4k,BC=5k,DC=6k(k>0).