题目内容
对于函数y=f(x),如果存在区间[m,n](m<n),当定义域是[m,n]时,f(x)的值域也是[m,n],则称f(x)在[m,n]上是“和谐函数”,且[m,n]为该函数的“和谐区间”.现有以下命题:
①f(x)=(x-1)2在[0,1]是“和谐函数”;
②恰有两个不同的正数a使f(x)=(x-1)2在[0,a]是“和谐函数”;
③f(x)=
+k对任意的k∈R都存在“和谐区间”;
④由方程x|x|+y|y|=1确定的函数y=f(x)必存在“和谐区间”.
其中正确的命题的个数是( )
①f(x)=(x-1)2在[0,1]是“和谐函数”;
②恰有两个不同的正数a使f(x)=(x-1)2在[0,a]是“和谐函数”;
③f(x)=
| 1 |
| x |
④由方程x|x|+y|y|=1确定的函数y=f(x)必存在“和谐区间”.
其中正确的命题的个数是( )
| A、1 | B、2 | C、3 | D、4 |
考点:函数的值域
专题:新定义,函数的性质及应用
分析:①结合二次函数f(x)的图象判定命题正确;
②由①得a=1时满足,讨论0<a<1,a>1时,是否有a满足;
③x>0时,若存在[m,n]为“和谐区间”,可得
,推出k=0有“和谐区间”,判定命题错误;
④x≥0且y≥0时,可得函数的“和谐区间”,判定命题正确.
②由①得a=1时满足,讨论0<a<1,a>1时,是否有a满足;
③x>0时,若存在[m,n]为“和谐区间”,可得
|
④x≥0且y≥0时,可得函数的“和谐区间”,判定命题正确.
解答:
解析:对①,结合二次函数f(x)=(x-1)2的图象得,命题正确;
对②,结合图象,由①,显然a=1满足,当0<a<1时都不满足,当a>1时,令(a-1)2=a,解得a=
,∴恰有两个不同的a满足题意,命题正确;
对③,考虑x>0时,若存在[m,n]为“和谐区间”,由单调递减性,可得
,
即
,两式相减得mn=1,∴k=0,
即只有k=0时才有“和谐区间”,∴命题错误;
对④,考虑x≥0且y≥0时,可得y=
,结合图象分析显然[0,1]为其“和谐区间”,∴命题正确;
综上,以上正确的有3个.
故选:C.
对②,结合图象,由①,显然a=1满足,当0<a<1时都不满足,当a>1时,令(a-1)2=a,解得a=
3+
| ||
| 2 |
对③,考虑x>0时,若存在[m,n]为“和谐区间”,由单调递减性,可得
|
即
|
即只有k=0时才有“和谐区间”,∴命题错误;
对④,考虑x≥0且y≥0时,可得y=
| 1-x2 |
综上,以上正确的有3个.
故选:C.
点评:本题考查了新定义的函数的性质与应用问题,解题时应理解新定义的问题是什么,结合题意进行解答,是易错题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
已知cosα=-
,α∈(
,π),则cos(
+α)=( )
| 4 |
| 5 |
| π |
| 2 |
| π |
| 2 |
A、-
| ||
B、
| ||
C、-
| ||
D、
|
已知a=log23+log2
,b=log23
,c=log32,则a,b,c的大小关系是( )
| 3 |
| 3 |
| A、a=b>c |
| B、a=b<c |
| C、a<b<c |
| D、a>b>c |
把函数f(x)=sin(2x-
)的图象向左平移φ(0<φ<π)个单位可以得到函数g(x)的图象,若g(x)的图象关于y轴对称,则φ的值为( )
| π |
| 3 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
从1,2,3…9这9个数中,取出4个数,其和为奇数的取法有( )
| A、20种 | B、40种 |
| C、60种 | D、80种 |
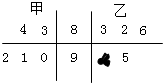 如图茎叶图表示的是甲、乙两人在5次综合测评中的成绩,其中一个数字被污损.则甲的平均成绩超过乙的平均成绩的概率为( )
如图茎叶图表示的是甲、乙两人在5次综合测评中的成绩,其中一个数字被污损.则甲的平均成绩超过乙的平均成绩的概率为( )A、
| ||
B、
| ||
C、
| ||
D、
|
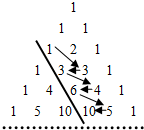 如图,在杨辉三角中,斜线l的上方从1按箭头方向可以构成一个“锯齿形”的数列{an}:1,3,3,4,6,5,10,…,记其前n项和为Sn,则S27的值为
如图,在杨辉三角中,斜线l的上方从1按箭头方向可以构成一个“锯齿形”的数列{an}:1,3,3,4,6,5,10,…,记其前n项和为Sn,则S27的值为