Question

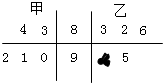如图茎叶图表示的是甲、乙两人在5次综合测评中的成绩，其中一个数字被污损．则甲的平均成绩超过乙的平均成绩的概率为（　　）

• A、

  1

  2

• B、

  2

  5

• C、

  1

  5

• D、

  1

  3

Answer 1

考点：众数、中位数、平均数

专题：概率与统计

分析：由茎叶图求出甲的平均成绩是88，设污损数字为x，乙的平均成绩为87.2+

x

5

，由题意知88＞87.2+

x

5

，由此能求出甲的平均成绩超过乙的平均成绩的概率．

解答： 解：由已知中的茎叶图可得
甲的5次综合测评中的成绩分别为83，84，90，91，92，
则甲的平均成绩：

1

5

（83+84+90+91+92）=88，
设污损数字为x
则乙的5次综合测评中的成绩分别为83，82，86，95，90+x
则乙的平均成绩：

1

5

（83+82+86+95+90+x）=87.2+

x

5

，
∵甲的平均成绩超过乙的平均成绩，
∴88＞87.2+

x

5

，解得x＜4，∴x=0，1，2，3，
∴甲的平均成绩超过乙的平均成绩的概率为：p=

4

10

=

2

5

．
故选：B．

点评：本题考查概率的求法，是基础题，解题时要认真审题，注意茎叶图的合理运用．