从1.2.3-9这9个数中.取出4个数.其和为奇数的取法有( ) A.20种B.40种C.60种D.80种题目和参考答案——青夏教育精英家教网—

题目内容

从1，2，3…9这9个数中，取出4个数，其和为奇数的取法有（　　）

A、20种	B、40种
C、60种	D、80种

考点：计数原理的应用

专题：排列组合

分析：根据题意，将这9个数分为奇数与偶数两个组，9分析可得，若取出的四个数的和为奇数，则取出的四个数必有1个或3个奇数；分别求出两种情况下的取法情况数，相加可得答案．

解答： 解：根据题意，将这9个数分为奇数与偶数两个组，
若取出的四个数的和为奇数，则取出的四个数必有1个或3个奇数；
若有1个奇数时，有C₅¹•C₄³=20种取法，
若有3个奇数时，有C₅³•C₄¹=40种取法，
故符合题意的取法共20+40=60种取法；
故选：C．

点评：本题考查利用组合解决常见计数问题的方法，解本题时，注意先分组，进而由组合的方法，结合乘法计数原理进行计算．

练习册系列答案

相关题目

对于函数y=f（x），如果存在区间[m，n]（m＜n），当定义域是[m，n]时，f（x）的值域也是[m，n]，则称f（x）在[m，n]上是“和谐函数”，且[m，n]为该函数的“和谐区间”．现有以下命题：
①f（x）=（x-1）²在[0，1]是“和谐函数”；
②恰有两个不同的正数a使f（x）=（x-1）²在[0，a]是“和谐函数”；
③f（x）=

+k对任意的k∈R都存在“和谐区间”；
④由方程x|x|+y|y|=1确定的函数y=f（x）必存在“和谐区间”．
其中正确的命题的个数是（　　）

设P是圆（x-3）²+（y+1）²=4上的动点，Q是直线x=-3上的定点（-3，-1），则|PQ|的最小值与最大值之和为（　　）

用数学归纳法证明等式：1+2+3…+3n=

9n2+3n

，由n=k的假设到证明n=k+1时，等式左边应添加的式子是（　　）

A、3k+1

B、（3k+1）+（3k+2）

C、3k+3

D、（3k+1）+（3k+2）+（3k+3）

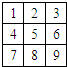用红、黄、蓝三种颜色去涂题图中标号为1，2，…，9的9个小正方形，使得任意相邻（有公共边）的小正方形所涂的颜色不同，且“3、5、7”号数字涂色相同，则符合条件的所有涂法种数为（　　）

A、96	B、108
C、196	D、432

已知集合M={x|x＜3}，N={x|2＜x＜4}，则M∩N=（　　）

二项式（x+2）¹⁰展开式中，二项式系数最大的项是（　　）

A、第5项	B、第6项
C、第7项	D、第5、6项

有50件产品编号从1到50，现在从中抽取5件检验，用系统抽样确定所抽取的样本编号可能为（　　）

试题分类