题目内容
已知抛物线x2=-4y的准线与双曲线
-
=1(a>0,b>0)的两条渐近线围成一个等腰直角三角形,则该双曲线的离心率是( )
| x2 |
| a2 |
| y2 |
| b2 |
A、
| ||
| B、5 | ||
C、
| ||
| D、2 |
考点:双曲线的简单性质
专题:圆锥曲线的定义、性质与方程
分析:由题意知双曲线的两条渐近线互相垂直,根据直线垂直斜率乘积等于-1,求出a与b的关系,再根据离心率公式计算即可.
解答:
解:因为抛物线x2=-4y的准线与双曲线
-
=1(a>0,b>0)的两条渐近线围成一个等腰直角三角形,
所以双曲线的两条渐近线互相垂直,
∵双曲线的渐近线为y=±
x
∴
•(-
)=-1
即a2=b2,
∴c=
=
a
∴e=
=
故选:C.
| x2 |
| a2 |
| y2 |
| b2 |
所以双曲线的两条渐近线互相垂直,
∵双曲线的渐近线为y=±
| b |
| a |
∴
| b |
| a |
| b |
| a |
即a2=b2,
∴c=
| a2+b2 |
| 2 |
∴e=
| c |
| a |
| 2 |
故选:C.
点评:本题主要考查了双曲线的性质,关键理解两条渐近线围成一个等腰直角三角形得到双曲线的两条渐近线互相垂直,属于中档题.

练习册系列答案
相关题目
有一长为1km的斜坡,它的倾斜角为20°,现要将倾斜角改为10°,则坡底要加长( )
| A、0.5km | ||||
| B、1km | ||||
| C、1.5km | ||||
D、
|
从1,2,3,4,5这5个数字中,任意抽取3个不同的数,这3个数的和为偶数的概率是( )
A、
| ||
B、
| ||
C、
| ||
D、
|
设P是圆(x-3)2+(y+1)2=4上的动点,Q是直线x=-3上的定点(-3,-1),则|PQ|的最小值与最大值之和为( )
| A、10 | B、8 | C、12 | D、14 |
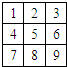 用红、黄、蓝三种颜色去涂题图中标号为1,2,…,9的9个小正方形,使得任意相邻(有公共边)的小正方形所涂的颜色不同,且“3、5、7”号数字涂色相同,则符合条件的所有涂法种数为( )
用红、黄、蓝三种颜色去涂题图中标号为1,2,…,9的9个小正方形,使得任意相邻(有公共边)的小正方形所涂的颜色不同,且“3、5、7”号数字涂色相同,则符合条件的所有涂法种数为( )| A、96 | B、108 |
| C、196 | D、432 |
在复平面内,复数z=
的共轭复数对应的点位于( )
| 2i-1 |
| i-1 |
| A、第一象限 | B、第二象限 |
| C、第三象限 | D、第四象限 |