题目内容
12.已知a>0,b>0,c>0,函数f(x)=|x+a|-|x-b|+c的最大值为10.(1)求a+b+c的值;
(2)求$\frac{1}{4}$(a-1)2+(b-2)2+(c-3)2的最小值,并求出此时a、b、c的值.
分析 (1)利用绝对值不等式,求出f(x)的最大值为a+b+c,即可求a+b+c的值;
(2)利用柯西不等式,即可得出结论.
解答 解:(1)f(x)=|x+a|-|x-b|+c≤|b+a|+c,当且仅当x≥b时等号成立,
∵a>0,b>0,∴f(x)的最大值为a+b+c.
又已知f(x)的最大值为10,所以a+b+c=10.(4分)
(2)由(1)知a+b+c=10,由柯西不等式得[$\frac{1}{4}$(a-1)2+(b-2)2+(c-3)2](22+12+12)≥(a+b+c-6)2=16,
即$\frac{1}{4}$(a-1)2+(b-2)2+(c-3)2≥$\frac{8}{3}$(7分)
当且仅当$\frac{1}{4}$(a-1)=b-2=c-3,即a=$\frac{11}{3}$,b=$\frac{8}{3}$,c=$\frac{11}{3}$时等号成立.(10分)
点评 本题考查绝对值不等式、柯西不等式的运用,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
相关题目
7.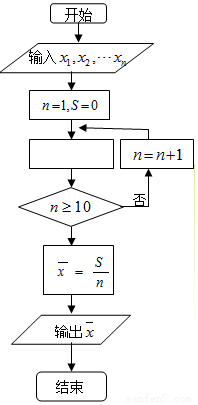 如图是求样本x1、x2、…x10平均数$\overline{x}$的程序框图,图中空白框中应填入的内容为( )
如图是求样本x1、x2、…x10平均数$\overline{x}$的程序框图,图中空白框中应填入的内容为( )
 如图是求样本x1、x2、…x10平均数$\overline{x}$的程序框图,图中空白框中应填入的内容为( )
如图是求样本x1、x2、…x10平均数$\overline{x}$的程序框图,图中空白框中应填入的内容为( )| A. | S=S+xn | B. | S=S+$\frac{{x}_{n}}{n}$ | C. | S=S+n | D. | S=S+$\frac{{x}_{n}}{10}$ |
1.执行如图所示的程序框图,则输出b的值为( )


| A. | 2 | B. | 4 | C. | 8 | D. | 16 |
 已知椭圆E:$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$(a>b>0)的离心率是$\frac{\sqrt{2}}{2}$,F1、F2是椭圆的左、右焦点,点A为椭圆的右顶点,点B为椭圆的上顶点,且S${\;}_{△AB{F}_{1}}$=$\frac{\sqrt{2}+1}{2}$.
已知椭圆E:$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$(a>b>0)的离心率是$\frac{\sqrt{2}}{2}$,F1、F2是椭圆的左、右焦点,点A为椭圆的右顶点,点B为椭圆的上顶点,且S${\;}_{△AB{F}_{1}}$=$\frac{\sqrt{2}+1}{2}$.