题目内容
8．已知数列{an}满足an+1=an+3，a1=0，则数列{an}的通项公式可以是（ ）| A． | n | B． | 2n | C． | 3n-3 | D． | 3n+3 |
分析 数列{an}是首项为0，公差为3的等差数列，由此能求出结果．
解答 解：∵数列{an}满足an+1=an+3，a1=0，
∴数列{an}是首项为0，公差为3的等差数列，
∴an=a1+（n-1）d=3n-3．
故选：C．
点评 本题考查数列的通项公式的求法，是基础题，解题时要认真审题，注意等差数列的性质的合理运用．
练习册系列答案
星级口算天天练系列答案
芒果教辅达标测试卷系列答案
相关题目
16．
如图，阴影部分的面积为（ ）
如图，阴影部分的面积为（ ）| A． | 9 | B． | $\frac{9}{2}$ | C． | $\frac{13}{6}$ | D． | $\frac{7}{3}$ |
3．
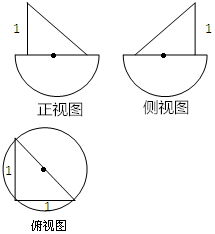已知某几何体的三视图如图所示，其中正视图、侧视图均由直角三角形中与半圆构成，俯视图由圆和内接三角形构成，根据图中的数据可得几何体的表面积为（ ）
已知某几何体的三视图如图所示，其中正视图、侧视图均由直角三角形中与半圆构成，俯视图由圆和内接三角形构成，根据图中的数据可得几何体的表面积为（ ）| A． | 1+$\frac{\sqrt{3}+3π}{2}$ | B． | $\frac{1+\sqrt{3}+π}{2}$ | C． | $\frac{1+\sqrt{3}+3π}{2}$ | D． | $\frac{3+\sqrt{3}+3π}{2}$ |
13．数列{an}满足an+1=$\left\{\begin{array}{l}{2{a}_{n}，0≤{a}_{n}≤\frac{1}{2}}\\{2{a}_{n}-1，\frac{1}{2}＜{a}_{n}≤1}\end{array}\right.$，若a1=$\frac{3}{5}$，则a2015=（ ）
| A． | $\frac{1}{5}$ | B． | $\frac{2}{5}$ | C． | $\frac{3}{5}$ | D． | $\frac{4}{5}$ |
17．已知全集U={x|x≤9，x∈N+}，集合A={1，2，3}，B={3，4，5，6}，则∁U（A∪B）=（ ）
| A． | {3} | B． | {7，8} | C． | {7，8，9} | D． | {1，2，3，4，5，6} |
18．曲线y=x2-1与直线y=2x+2轴围成的封闭部分的面积为（ ）
| A． | $\frac{17}{3}$ | B． | $\frac{22}{3}$ | C． | $\frac{32}{3}$ | D． | $\frac{35}{3}$ |