题目内容
5.关于函数$f(x)=\sqrt{3}{cos^2}x+2sinxcosx-\sqrt{3}{sin^2}x$,有如下问题:①$x=\frac{π}{12}$是f(x)的图象的一条对称轴;
②$?x∈R,f({\frac{π}{3}+x})=-f({\frac{π}{3}-x})$;
③将f(x)的图象向右平移$\frac{π}{3}$个单位,可得到奇函数的图象;
④?x1,x2∈R,|f(x1)-f(x2)|≥4.
其中真命题的个数是( )
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
分析 利用辅助角公式将函数f(x)化简,结合三角函数的图象及性质依次对各项进行判断即可.
解答 解:函数$f(x)=\sqrt{3}{cos^2}x+2sinxcosx-\sqrt{3}{sin^2}x$,
化简可得:f(x)=$\sqrt{3}$cos2x+sin2x=2sin(2x+$\frac{π}{3}$),
对于①:当x=$\frac{π}{12}$时,函数f(x)取得最大值2,∴x=$\frac{π}{12}$是其中一条对称轴.故①对.
对于②:f(x+$\frac{π}{3}$)=2sin(2x+$\frac{π}{3}$+$\frac{2π}{3}$)=-2sin2x,
-f($\frac{π}{3}$-x)=-2sin(-2x+$\frac{π}{3}$+$\frac{2π}{3}$)=-2sin2x,
∴$?x∈R,f({\frac{π}{3}+x})=-f({\frac{π}{3}-x})$;故②对.
对于③将f(x)的图象向右平移$\frac{π}{3}$个单位,可得2sin[2(x$-\frac{π}{3}$)+$\frac{π}{3}$]=2sin(2x-$\frac{π}{3}$)不是奇函数,故③不对
④?x1,x2∈R,|f(x1)-f(x2)|≥4.
f(x)=2sin(2x+$\frac{π}{3}$),当x1=$\frac{π}{6}$,${x}_{2}=-\frac{5π}{12}$时,|f(x1)-f(x2)|=4,存在x1,x2∈R使得|f(x1)-f(x2)|≥4,故④对.
∴真命题的个数是3.
故选:C.
点评 本题主要考查三角函数的图象和性质,利用三角函数公式将函数进行化简是解决本题的关键.

练习册系列答案
相关题目
15.某民调机构为了了解民众是否支持英国脱离欧盟,随机抽调了100名民众,他们的年龄的频数及支持英国脱离欧盟的人数分布如下表:
(Ⅰ)由以上统计数据填下面列联表,并判断是否有99%的把握认为以50岁胃分界点对是否支持脱离欧盟的态度有差异;
附:${K^2}=\frac{{n{{(ad-bc)}^2}}}{(a+b)(c+d)(a+c)(b+d)}$
(Ⅱ)若采用分层抽样的方式从18-64岁且支持英国脱离欧盟的民众中选出7人,再从这7人中随机选出2人,求这2人至少有1人年龄在18-24岁的概率.
| 年龄段 | 18-24岁 | 25-49岁 | 50-64岁 | 65岁及以上 |
| 频数 | 35 | 20 | 25 | 20 |
| 支持脱欧的人数 | 10 | 10 | 15 | 15 |
| 年龄低于50岁的人数 | 年龄不低于50岁的人数 | 合计 | |
| 支持“脱欧”人数 | |||
| 不支持“脱欧”人数 | |||
| 合计 |
| P(K2≥k0) | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 |
| K0 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 |
20.已知变量x与y的取值如表所示,且2.5<n<m<6.5,则由该数据算得的线性回归方程可能是( )
| x | 2 | 3 | 4 | 5 |
| y | 6.5 | m | n | 2.5 |
| A. | $\stackrel{∧}{y}$=0.8x+2.3 | B. | $\stackrel{∧}{y}$=2x+0.4 | C. | $\stackrel{∧}{y}$=-1.5x+8 | D. | $\stackrel{∧}{y}$=-1.6x+10 |
10.已知某企业的近3年的前7个月的月利润(单位:百万元)如下面的折线图所示:
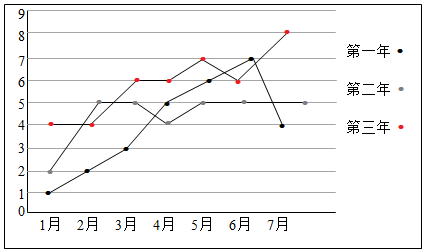
(1)试问这3年的前7个月中哪个月的月平均利润较高?
(2)通过计算判断这3年的前7个月的总利润的发展趋势;
(3)试以第3年的前4个月的数据(如下表),用线性回归的拟合模式估测第3年8月份的利润.
相关公式:$\widehat{b}$=$\frac{\sum_{i=1}^{n}({x}_{i}-\overline{x})({y}_{i}-\overline{y})}{\sum_{i=1}^{n}({x}_{i}-\overline{x})^{2}}$=$\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{x}\overline{y}}{\sum_{i=1}^{n}{{x}_{i}}^{2}-n(\overline{x})^{2}}$,$\widehat{a}$=$\widehat{y}$-$\widehat{b}$x.

(1)试问这3年的前7个月中哪个月的月平均利润较高?
(2)通过计算判断这3年的前7个月的总利润的发展趋势;
(3)试以第3年的前4个月的数据(如下表),用线性回归的拟合模式估测第3年8月份的利润.
| 月份x | 1 | 2 | 3 | 4 |
| 利润y(单位:百万元) | 4 | 4 | 6 | 6 |
8.已知数列{an}满足an+1=an+3,a1=0,则数列{an}的通项公式可以是( )
| A. | n | B. | 2n | C. | 3n-3 | D. | 3n+3 |
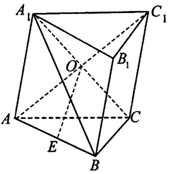 如图,在斜三梭柱ABC-A1B1C1中,侧面AA1C1C是菱形,AC1与A1C交于点O,E是棱AB上一点,且OE∥平面BCC1B1
如图,在斜三梭柱ABC-A1B1C1中,侧面AA1C1C是菱形,AC1与A1C交于点O,E是棱AB上一点,且OE∥平面BCC1B1