题目内容

15．已知两定点F1（-5，0），F2（5，0），动点P到这两定点距离差为6，则点的轨迹方程是$\frac{{x}^{2}}{9}-\frac{{y}^{2}}{16}$=1（x≥3）．

分析 由条件知，点P的轨迹是以F1、F2为焦点的双曲线右支，从而写出轨迹的方程即可．

解答 解：由|PF1|-|PF2|=6＜|F1F2|知，点P的轨迹是以F1、F2为焦点的双曲线右支，
得c=5，2a=6，
∴a=3，
∴b2=16，
故动点P的轨迹方程是$\frac{{x}^{2}}{9}-\frac{{y}^{2}}{16}$=1（x≥3）．
故答案为：$\frac{{x}^{2}}{9}-\frac{{y}^{2}}{16}$=1（x≥3）．

点评 本题考查双曲线的定义、求双曲线的标准方程，体现了等价转化的数学思想．

练习册系列答案
相关题目
5．抛物线的标准方程是y2=-12x，则其焦点坐标是（　　）
A．（3，0）B．（-3，0）C．（0，3）D．（0，-3）
6．（1）已知正数x、y满足xy=x+y+3，试求xy、x+y的范围．
（2）已知x＞0，求证：x+$\frac{1}{x}$+$\frac{1}{x+\frac{1}{x}}$≥$\frac{5}{2}$．
3．已知函数f（x）=Asin（ωx-$\frac{π}{3}$）+1（A＞0，ω＞0）的最大值为3，其图象相邻两条对称轴之间的距离是$\frac{π}{2}$．
（1）求f（x）的解析式：
（2）求f（x）的在[0，π]上的单增区间：
（3）若f（$\frac{α}{2}$）＞2，求α的取值范围．
10．若以原点O为圆心的圆同时经过椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）的左顶点A1及右顶点A2，且被过焦点F（c，0）的直线l：x=c分成弧长为2：1的两端圆弧，则该椭圆的离心率e等于$\frac{1}{2}$．
20．已知向量$\overrightarrow{OA}$，$\overrightarrow{OB}$，$\overrightarrow{OC}$满足条件$\overrightarrow{OA}$+$\overrightarrow{OB}$+$\overrightarrow{OC}$=0，|$\overrightarrow{OA}$|=|$\overrightarrow{OB}$|=|$\overrightarrow{OC}$|=1，求证：△ABC为正三角形．
7．如图，在平行四边形ABCD中，设$\overrightarrow{AB}$=$\overrightarrow{a}$，$\overrightarrow{AD}$=$\overrightarrow{b}$，试用$\overrightarrow{a}$，$\overrightarrow{b}$表示向量$\overrightarrow{AC}$、$\overrightarrow{BD}$．
4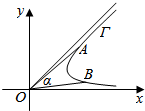．如图，在平面直角坐标系xOy中，对于曲线Γ，若存在以O为顶点的角α，使得α≥∠AOB对于曲线π上的任意两个不同的点A，B恒成立，则称角α为曲线的相对于点O的“渐近角”并称其中最小的“渐近角”为曲线Γ的相对于点O的“望角”．已知曲线C：y=$\left\{\begin{array}{l}{2x{e}^{x-1}+2，x＞0}\\{\frac{\sqrt{36+25{x}^{2}}}{3}，x≤0}\end{array}\right.$（其中e=2.71828…是自然对数的底数），则曲线C的相对于点O的“望角”为（　　）
A．$\frac{3π}{4}$B．$\frac{2π}{3}$C．$\frac{π}{3}$D．$\frac{π}{4}$
5．求经过A（6，0），B（5，-3），C（3，1）三点的圆的方程．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网