Question

4．如图，在平面直角坐标系xOy中，对于曲线Γ，若存在以O为顶点的角α，使得α≥∠AOB对于曲线π上的任意两个不同的点A，B恒成立，则称角α为曲线的相对于点O的“渐近角”并称其中最小的“渐近角”为曲线Γ的相对于点O的“望角”．已知曲线C：y=$\left\{\begin{array}{l}{2x{e}^{x-1}+2，x＞0}\\{\frac{\sqrt{36+25{x}^{2}}}{3}，x≤0}\end{array}\right.$（其中e=2.71828…是自然对数的底数），则曲线C的相对于点O的“望角”为（　　）

• A． $\frac{3π}{4}$
• B． $\frac{2π}{3}$
• C． $\frac{π}{3}$
• D． $\frac{π}{4}$

Answer 1

分析 画出函数f（x）的图象，过点O作出两条直线与曲线无限接近，当x≤0时，曲线y=$\frac{\sqrt{36+25{x}^{2}}}{3}$与直线y=k₁x无限接近，考虑渐近线，求出k₁=-$\frac{5}{3}$；当x＞0时，设出切点，求出切线的斜率，列出方程，求出切点（1，2），即得k₂=4，再由两直线的夹角公式即可得到所求的“望角”．

解答 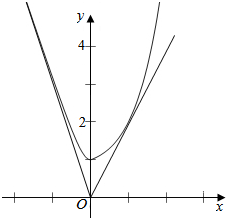解：画出函数f（x）的图象，过点O作出两条直线与曲线无限接近，设它们的方程分别为y=k₁x，y=k₂x，
当x≤0时，曲线y=$\frac{\sqrt{36+25{x}^{2}}}{3}$与直线y=k₁x无限接近，即为双曲线的渐近线，故k₁=-$\frac{5}{3}$；
当x＞0时，y=2xe^x-1+2，x＞0，y′=2e^x-1+2xe^x-1，设切点为（m，n），则n=k₂m，
n=2me^m-1+2，k₂=2e^m-1+2me^m-1，即有m²e^m-1=1，
由2xe^x-1（x＞0）为增函数，且x=1成立，故m=1，k₂=4，
由两直线的夹角公式得，tanθ=|$\frac{4+\frac{5}{3}}{1-\frac{5}{3}×4}$|=1，
故曲线C相对于点O的“望角”为$\frac{π}{4}$．
故选：D．

点评 本题考查新定义“望角”及应用，考查导数的应用：求切线，双曲线的性质：渐近线，属于中档题．