题目内容
1.已知x,y满足$\left\{\begin{array}{l}{y≥x}\\{x+y≤2}\\{x≥\frac{1}{4}}\end{array}\right.$且z=2x+y的最大值与最小值分别为a和b,则a-b的值是$\frac{9}{4}$.分析 通过计算出三个交点的坐标,进而计算出z的最大值与最小值,从而可得结论.
解答 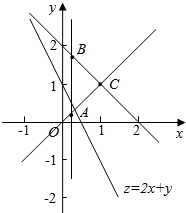 解:依题意,易知A($\frac{1}{4}$,$\frac{1}{4}$),B($\frac{1}{4}$,$\frac{7}{4}$),C(1,1),
解:依题意,易知A($\frac{1}{4}$,$\frac{1}{4}$),B($\frac{1}{4}$,$\frac{7}{4}$),C(1,1),
又∵zA=$2×\frac{1}{4}+\frac{1}{4}$=$\frac{3}{4}$,
zB=$2×\frac{1}{4}+\frac{7}{4}$=$\frac{9}{4}$,
zC=2×1+1=3,
∴a=3,b=$\frac{3}{4}$,
∴a-b=3-$\frac{3}{4}$=$\frac{9}{4}$,
故答案为:$\frac{9}{4}$.
点评 本题考查简单线性规划,考查运算求解能力、数形结合,注意解题方法的积累,属于中档题.

练习册系列答案
 小学夺冠AB卷系列答案
小学夺冠AB卷系列答案 ABC考王全优卷系列答案
ABC考王全优卷系列答案
相关题目
12.已知命题p:“?x>0,有ex≥1成立,则¬p为( )
| A. | ?x0≤0,有ex0<l成立 | B. | ?x0≤0,有ex0≥1成立 | ||
| C. | ?x0>0,有ex0<1成立 | D. | ?x0>0,有ex0≤l成立 |
9.下列各组函数中,表示同一函数的是( )
| A. | f(x)=$\root{5}{{x}^{5}}$与f(x)=$\sqrt{{x}^{2}}$ | B. | y=x与$y=\root{3}{x^3}$ | ||
| C. | $y=\frac{(x-1)(x+3)}{x-1}$与y=x+3 | D. | y=1与y=x0 |
16.已知△ABC的角A,B,C所对的边分别为a,b,c,∠C=90°,则$\frac{a+b}{c}$的取值( )
| A. | (0,2) | B. | $({0,\sqrt{2}}]$ | C. | $({1,\sqrt{2}}]$ | D. | $[{1,\sqrt{2}}]$ |
13.等差数列{an}的前m项和为30,前2m项和为100,则它的前3m项和为( )
| A. | 70 | B. | 130 | C. | 140 | D. | 210 |
10.设θ是三角形的内角,下列各对数中均取正值的是 ( )
| A. | tanθ和cosθ | B. | cosθ和cotθ | C. | sinθ和secθ | D. | cot$\frac{θ}{2}$和sinθ |