题目内容
已知全集U=R，集合A={x|0＜x≤5}，B={x|x＜-3或x＞1}，C={x|[x-（a-1）][x-（a+1）]＜0，a∈R}．
（1）求A∩B，（∁UA）∩（∁UB），∁U（A∩B）；
（2）若（∁RA）∩C=∅，求a的取值范围．
（1）求A∩B，（∁UA）∩（∁UB），∁U（A∩B）；
（2）若（∁RA）∩C=∅，求a的取值范围．
考点：交、并、补集的混合运算
专题：集合
分析：（1）根据集合的基本运算即可求A∩B，（∁UA）∩（∁UB），∁U（A∩B）；
（2）根据条件（∁RA）∩C=∅，建立条件关系即可求a的取值范围．
（2）根据条件（∁RA）∩C=∅，建立条件关系即可求a的取值范围．
解答：
解：（1）∵A={x|0＜x≤5}，B={x|x＜-3或x＞1}，
∴A∩B={x|1＜x≤5}，（∁UA）∩（∁UB）={x|x＞5或x≤0}∩{x|-3≤x≤1}={x|-3≤x≤0}，
∁U（A∩B）={x|x5＞或x≤1}；
（2）∵∁UA={x|x＞5或x≤0}，C={x|[x-（a-1）][x-（a+1）]＜0，a∈R}={x|a-1＜x＜a+1}．
∴
，即
，
解得1≤a≤4．
∴A∩B={x|1＜x≤5}，（∁UA）∩（∁UB）={x|x＞5或x≤0}∩{x|-3≤x≤1}={x|-3≤x≤0}，
∁U（A∩B）={x|x5＞或x≤1}；
（2）∵∁UA={x|x＞5或x≤0}，C={x|[x-（a-1）][x-（a+1）]＜0，a∈R}={x|a-1＜x＜a+1}．
∴
|
|
解得1≤a≤4．
点评：本题主要考查集合的基本运算，要求熟练掌握集合的交，并，补运算．
练习册系列答案
培优口算题卡系列答案
开心口算题卡系列答案
口算题卡河北少年儿童出版社系列答案
相关题目
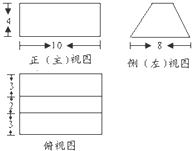
某几何体的三视图如图所示，则该几何体的体积为（ ）
| A、240 | ||
| B、200 | ||
C、
| ||
D、
|
下列四组中的f（x），g（x），表示同一个函数的是（ ）
| A、f（x）=1，g（x）=x0 | ||
B、f（x）=x-1，g（x）=
| ||
C、f（x）=x，g（x）=（
| ||
D、f（x）=|1-2x|，g（x）=
|