题目内容
4.${e^{-2}},{2^{\frac{1}{e}}},ln2$三个数中最大的数是${2^{\frac{1}{e}}}$.分析 利用指数函数与对数函数的单调性即可得出.
解答 解:∵e-2∈(0,1),${2}^{\frac{1}{e}}$>1,ln2∈(0,1),
因此三个数中最大的数是${2^{\frac{1}{e}}}$.
故答案为:${2^{\frac{1}{e}}}$.
点评 本题考查了指数函数与对数函数的单调性,考查了推理能力与计算能力,属于基础题.

练习册系列答案
 捷径训练检测卷系列答案
捷径训练检测卷系列答案 小夫子全能检测系列答案
小夫子全能检测系列答案
相关题目
14.已知平面向量$\overrightarrow{a}$=(1,0),$\overrightarrow{b}$=(-$\frac{1}{2}$,$\frac{\sqrt{3}}{2}$),则$\overrightarrow{a}$与$\overrightarrow{a}$+$\overrightarrow{b}$的夹角为( )
| A. | $\frac{π}{6}$ | B. | $\frac{π}{3}$ | C. | $\frac{2π}{3}$ | D. | $\frac{5π}{6}$ |
19.一个几何体的三视图如图所示,则这个几何体的直观图为( )
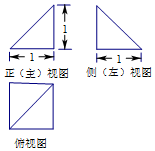

| A. | 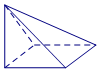 | B. | 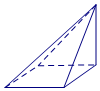 | C. | 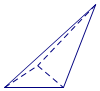 | D. | 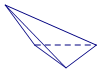 |
16.已知某四棱锥的三视图如右图所示,则该几何体的体积为( )
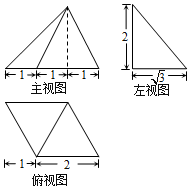

| A. | $\frac{{2\sqrt{3}}}{3}$ | B. | $\frac{{4\sqrt{3}}}{3}$ | C. | 2 | D. | $\frac{{5\sqrt{3}}}{3}$ |
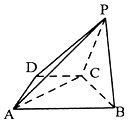 如图,已知四棱锥P-ABCD中,底面ABCD是直角梯形,∠ADC=90°,AB∥CD,AD=DC=$\frac{1}{2}$AB=$\sqrt{2}$,平面PBC⊥平面ABCD.
如图,已知四棱锥P-ABCD中,底面ABCD是直角梯形,∠ADC=90°,AB∥CD,AD=DC=$\frac{1}{2}$AB=$\sqrt{2}$,平面PBC⊥平面ABCD.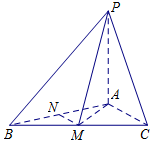 在三棱锥P-ABC中,PA⊥平面ABC,AB=AC=2,BC=2$\sqrt{3}$,M,N分别为BC,AB中点.
在三棱锥P-ABC中,PA⊥平面ABC,AB=AC=2,BC=2$\sqrt{3}$,M,N分别为BC,AB中点. 某次比赛甲得分的茎叶图如图所示,若去掉一个最高分,去掉一个最低分,则剩下4个分数的方差为14.
某次比赛甲得分的茎叶图如图所示,若去掉一个最高分,去掉一个最低分,则剩下4个分数的方差为14.